题目内容
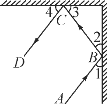
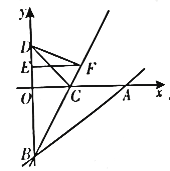
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)P(
;(2)P(![]() );(3)存在这样的H点使之成立;
);(3)存在这样的H点使之成立;![]() ,
,![]() ,
,![]()
【解析】
(1)根据翻折求出点A的坐标,代入即可求得;
(2)求出直线AE和直线BC的解析式,联立可求出点P的坐标;
(3)分两种情况,当点H在x轴上和在y轴上分析.
(1) 对于直线![]() ,
,
当x=0时,y=-6,
又∵D(0,4),
∴BD=10,
由翻折知AB=BD=10,
根据勾股定理得OA=![]() =
=![]() =8,
=8,
∴A(8,0),
把A(8,0)代入![]() 得k=
得k=![]() ,
,
∴y=![]()
(2)过点D作BC的对称点A(8,0),
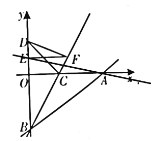
∵E(0,3) ,
∴直线AE的解析式为y=-![]() x+3,
x+3,
∵A,D关于BC对称,
∴OP=OP,![]() PDE的周长=DE+DP+EP,
PDE的周长=DE+DP+EP,
设OC=x,则CD=CA=8-x,
在Rt△DOC中,x+4=(8-x),解得x=3,
∴C(3,0)
∵C(3,0),B(0,-6),
∴直线BC的解析式为y=2x-6,
联立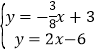 ,解得
,解得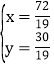 ,
,
∴P(![]() );
);
(3) 存在这样的H点使之成立,
∵![]() =
=![]() ×AC×BO=
×AC×BO=![]() ×5×6=15,
×5×6=15,
∴当点H在x轴上时,得![]() ;
;
当点H在y轴上时,设H(0,a),
∵![]() =
=![]() ∣a+6∣·8=15,即a=-
∣a+6∣·8=15,即a=-![]() 或-
或-![]() ,
,
∴综上,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目