题目内容
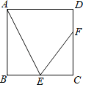
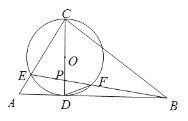
【题目】如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.
(1)求证:AB与⊙O相切;
(2)若AD=4,BD=6,则⊙O的半径= ;
(3)若PC=2PF,BF=a,求CP(用a的代数式表示).
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明∠CDF+∠FDB=90°,即∠CDB=90°,即可证明AB与⊙O相切;
(2)证明△CBD∽△ADC,求出CD=2![]() ,即可得出⊙O的半径;
,即可得出⊙O的半径;
(3)证明△PCF∽△PBC,得出![]() ,根据已知可得PF=
,根据已知可得PF=![]() BF=
BF=![]() a,从而得到CP的值.
a,从而得到CP的值.
解:(1)∵∠ACB=90°
∴∠CBE+∠CEB=90°
∵∠ABC=∠EFD,
∠ABC=∠CBE+∠FBD
∠EFD=∠FDB+∠FBD
∴∠CBE=∠FDB
∵∠CEB=∠CDF
∴∠CDF+∠FDB=90°
即∠CDB=90°
∴AB与⊙O相切.
(2)∵∠ACD+∠BCD=90°
∠ACD+∠A=90°
∴∠BCD=∠A
∵∠BCD=∠ADC=90°
∴△CBD∽△ADC
∴![]()
∴CD2=AD![]() BD=4×6=24
BD=4×6=24
∴CD=2![]()
即⊙O的直径为2![]()
∴⊙O的半径为![]() .
.
故答案为![]() .
.
(3)∵CD是⊙O的直径
∴∠CFD=90°
∴∠CDF+∠DCF=90°
∵∠CDB=90°
∴∠CDF+∠FDB=90°
∴∠DCF=∠FDB
∵∠EBC=∠FDB
∴∠EBC=∠DCF
∴△PCF∽△PBC
∴![]()
∴PB=2PC=4PF
∵PB=BF+PF
∴PF=![]() BF=
BF=![]() a
a
∴PC=2PF=![]() a
a
故答案为![]() .
.

【题目】某中学号召全校学生进行安全教育网络学习,并对部分学生的学习情况进行了随机调查.对部分学生的成绩(x为整数,满分100分)进行统计,并绘制了如下统计图表.
调查结果频数分布表
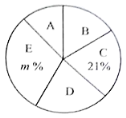
| 调查结果扇形统计图
|
根据所给信息,解答下列问题:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形统计图中,m的值及A组对应的圆心角的度数;
(3)若参加学习的同学共有1500人,请你估计成绩不低于80分的同学有多少人.