题目内容
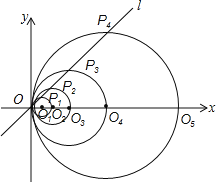
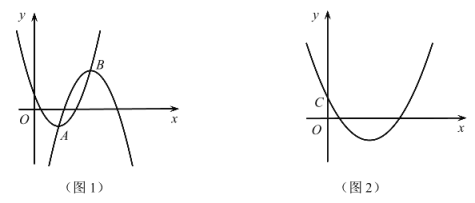
【题目】(如图 1,若抛物线 l1 的顶点 A 在抛物线 l2 上,抛物线 l2 的顶点 B 也在抛物线 l1 上(点 A 与点 B 不重合).我们称抛物线 l1,l2 互为“友好”抛物线,一条抛物线的“友 好”抛物线可以有多条.
(1)如图2,抛物线 l3:![]() 与y 轴交于点C,点D与点C关于抛物线的对称轴对称,则点 D 的坐标为 ;
与y 轴交于点C,点D与点C关于抛物线的对称轴对称,则点 D 的坐标为 ;
(2)求以点 D 为顶点的 l3 的“友好”抛物线 l4 的表达式,并指出 l3 与 l4 中y 同时随x增大而增大的自变量的取值范围;
(3)若抛物线 y=a1(x-m)2+n 的任意一条“友好”抛物线的表达式为 y=a2(x-h)2+k, 写出 a1 与a2的关系式,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的函数表达式为
的函数表达式为![]() ,
,![]() ;(3)
;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)设x=0,求出y的值,即可得到C的坐标,根据抛物线L3:![]() 得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;
得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;
(2)由(1)可知点D的坐标为(4,1),再由条件以点D为顶点的L3的“友好”抛物线L4的解析式,可求出L4的解析式,进而可求出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得(a1+a2)(h-m)2=0.可得![]() .
.
解:(1)∵抛物线l3:![]() ,
,
∴顶点为(2,-1),对称轴为x=2,
设x=0,则y=1,
∴C(0,1),
∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,1);
(2)解:设![]() 的函数表达式为
的函数表达式为![]()
由“友好”抛物线的定义,过点![]()
![]()
![]()
![]() 的函数表达式为
的函数表达式为![]()
![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量的取值范围是
增大而增大的自变量的取值范围是![]()
(3)![]()
理由如下:
∵ 抛物线![]() 与抛物线
与抛物线![]() 互为“友好”抛物线,
互为“友好”抛物线,
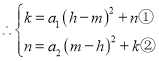
①+②得:![]()
![]()
![]()

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案