题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
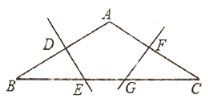
【答案】EG=5cm.
【解析】
连接AE、AG,根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,再根据等腰三角形两底角相等求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEG=60°,同理求出∠AGE=60°,从而判断出,△AEG为等边三角形,再根据等边三角形三边都相等列式求解即可.
如图,连接AE、AG,
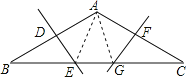
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B=![]() =30°,
=30°,
∴∠BAE=30°,
∴∠AEG=60°,
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG,
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又BE+EG+GC=BC=15(cm),
∴EG=5(cm).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目