题目内容
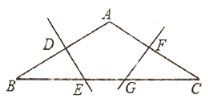
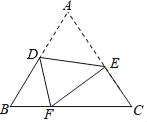
【题目】如图,把等边△ABC沿DE翻折,使点A落在BC上的F处,给出以下结论:
①∠BDF=∠EFC;
②BDCE=BFCF;
③S△BDF+S△EFC=![]() ;
;
④若BF:CF=1:2,则AD:AE=4:5.其中正确的结论有_____.(填序号)
【答案】①②④.
【解析】
①根据∠CFE+∠DFE=120°,∠BDF+∠DFB=120°,即可得到∠BDF=∠EFC;②根据△BDF∽△CFE,可得![]() ,即可得BDCE=BFCF;③当点F为BC的中点时,S△BDF+S△EFC=
,即可得BDCE=BFCF;③当点F为BC的中点时,S△BDF+S△EFC=![]() 成立,当点E与点C重合,点F与点B重合时,S△BDF+S△EFC=0;④设BF=1,CF=2,则BC=3=AB=AC,设DF=x=AD,则BD=3﹣x,依据
成立,当点E与点C重合,点F与点B重合时,S△BDF+S△EFC=0;④设BF=1,CF=2,则BC=3=AB=AC,设DF=x=AD,则BD=3﹣x,依据![]() ,可得CE=
,可得CE=![]() ,再根据相似三角形的对应边成比例,即可得到
,再根据相似三角形的对应边成比例,即可得到![]() ,进而得到AD:AE=4:5.
,进而得到AD:AE=4:5.
①由折叠可得,∠DFE=∠A=60°,
∴∠CFE+∠DFE=120°,
∵∠B=60°,
∴∠BDF+∠DFB=120°,
∴∠BDF=∠EFC,故①正确;
②∵∠B=∠C=60°,∠BDF=∠EFC,
∴△BDF∽△CFE,
∴![]() ,
,
即BDCE=BFCF,故②正确;
③当点F为BC的中点时,S△BDF+S△EFC=![]() 成立,
成立,
当点E与点C重合,点F与点B重合时,S△BDF+S△EFC=0,
此时,S△BDF+S△EFC=![]() 不成立,故③错误;
不成立,故③错误;
④设BF=1,CF=2,则BC=3=AB=AC,
设DF=x=AD,则BD=3﹣x,
由![]() ,可得
,可得![]() ,
,
解得CE=![]() ,
,
∴AE=3﹣![]() =EF,
=EF,
由![]() ,可得
,可得![]() ,
,
解得x=![]() ,
,
∴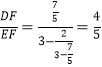 ,
,
∴AD:AE=4:5,故④正确.
故答案为:①②④.

练习册系列答案
相关题目