Question

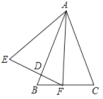
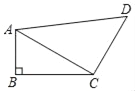
【题目】如图，四边形ABCD中，∠B＝90°，∠ACB＝30°，AB＝2，CD＝3，AD＝5．

（1）求证：AC⊥CD；

（2）求四边形ABCD的面积．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）根据直角三角形的性质得到AC=2AB=4，根据跟勾股定理的逆定理即可得到结论；

（2）根据勾股定理得到BC，根据三角形的面积公式即可得到结论．

（1）在Rt△ABC中，∠B=90°，∠ACB=30°，AB=2，∴AC=2AB=4．在△ACD中，AC=4，CD=3，AD=5．

∵42+32=52，即AC2+CD2=AD2，∴∠ACD=90°，∴AC⊥CD；

（2）在Rt△ABC中，∠B=90°，AB=2，AC=4，∴BC，∴Rt△ABC的面积为ABBC2×2．

又∵Rt△ACD的面积为ACCD4×3=6，∴四边形ABCD的面积为：26．