题目内容
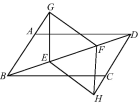
【题目】如图,在ABCD中,E,F是对角线BD上的两点,BE=DF,点G,H分别在BA和DC的延长线上,且AG=CH,连接GE,EH,HF,FG.
(1)求证:四边形GEHF是平行四边形;
(2)若点G,H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
【答案】(1)见解析;(2)仍成立.
【解析】
(1)先由平行四边形的性质,得AB=CD,AB∥CD,根据两直线平行内错角相等得∠GBE=∠HDF.再由SAS可证△GBE≌△HDF,利用全等的性质,证明∠GEF=∠HFE,从而得GE∥HF,又GE=HF,运用一组对边平行且相等的四边形是平行四边形得证.
(2)仍成立.可仿照(1)的证明方法进行证明.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠GBE=∠HDF.
又∵AG=CH,∴BG=DH.
又∵BE=DF,∴△GBE≌△HDF.
∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE,
∴GE∥HF,∴四边形GEHF是平行四边形.
(2)解:仍成立.(证法同上)

练习册系列答案
相关题目