题目内容
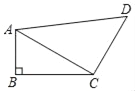
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
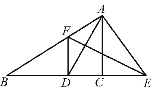
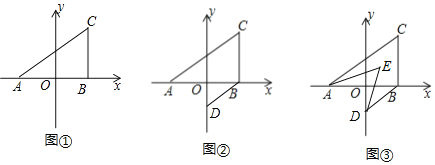
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;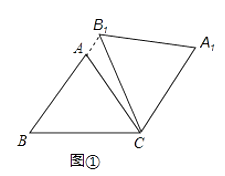
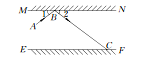
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.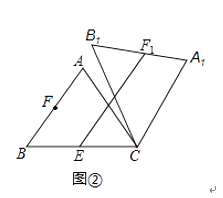
【答案】
(1)①证明:∵AB=AC,B1C=BC,
∴∠BB1C=∠B,∠B=∠ACB,
∵∠A1CB1=∠ACB(旋转角相等),
∴∠BB1C=∠A1CB1,
∴BB1∥CA1,
②过A作AF⊥BC于F,过C作CE⊥AB于E,
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=0.6,AB=5,
∴BF=3,
∴BC=6∴B1C=BC=6
∵CE⊥AB,
∴BE=B1E= ![]() ×6=
×6= ![]() ,
,
∴BB1= ![]() ,CE=
,CE= ![]() ,
,
∴AB1= ![]() ,
,
∴△AB1C的面积为: ![]() =
= ![]()
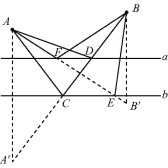
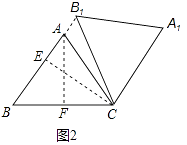
(2)如图3,
过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值.
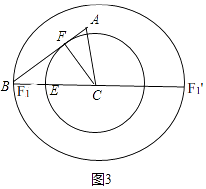
此时在Rt△BFC中,CF=4.8,
∴CF1=4.8,
∴EF1的最小值为4.8﹣3=1.8;
如图,以C为圆心BC为半径画圆交BC的延长线于F1',EF1'有最大值.
此时EF1'的最大值为EC+CF1'=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣1.8=7.2.
【解析】(1)①根据旋转的性质和平行线的性质证明;②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质和三角形的面积公式解答;(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,以C为圆心BC为半径画圆交BC于F1,得出最大和最小值解答即可。
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.

【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
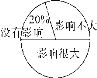
人数统计表如下:
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)