��Ŀ����
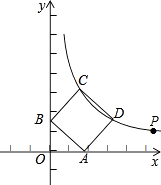
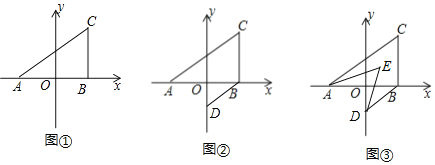
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��AOC=60������һֱ�����ǰ�MON��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
��1�����CON�Ķ�����
��2����ͼ2�ǽ�ͼ1�е����ǰ��Ƶ�O��ÿ��15�����ٶ�����ʱ�뷽����תһ�ܵ����������ת�Ĺ����У���t��ʱ����������OA��OC��OM����������ȵĽǣ����ʱ��tֵ
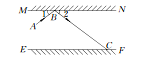
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ⲿ����ͼ4��ʹON�ڡ�AOC���ڲ�����ֱ�̽����AOM���NOC֮���������ϵ����˵�����ɣ�
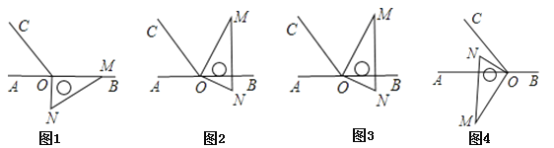
���𰸡���1��150�㣻��2��tΪ4��16��10��22�룻��3��ON�ڡ�AOC���ⲿʱ����NOC -��AOM=30����ON�ڡ�AOC���ڲ�ʱ����AOM-��NOC=30�������ɼ�����
��������
��1�����ݽǵĺͲ�ɵõ����ۣ�
��2����ͼ2�У�������������ۣ��ٵ���COMΪ60��ʱ���ڵ���AOMΪ60��ʱ���۵�OM��ƽ�֡�AOCʱ���ܵ�OM�����ӳ���ƽ�֡�AOCʱ�����ݽǵĺͲ�ɵõ����ۣ�
��3��ON�ڡ�AOC���ⲿʱ�͵�ON�ڡ�AOC�ڲ�ʱ���ֱ���ݽǵĺͲ�ɵõ����ۣ�
(1)��֪��AOC=60����MO��ON��
���AON=90����
���CON=��AON+��AOC=150����
(2)�ߡ�AOC=60����
�ٵ���COMΪ60��ʱ��
��תǰ��COMΪ120���������ǰ�MON��ʱ����ת��60������ת��![]() 4�룻
4�룻
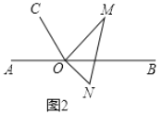
�ڵ���AOMΪ60��ʱ��
��תǰ��AOMΪ180����OM����OC�غϣ�
�����ǰ�MON��ʱ����ת��240������ת��![]() 16�룻
16�룻
�۵�OM��ƽ�֡�AOCʱ��
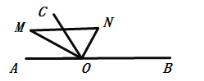
��MOB=180��-30��=150���������ǰ�MON��ʱ����ת��150������ת��![]() 10�룻
10�룻
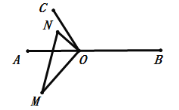
�ܵ�OM�����ӳ���ƽ�֡�AOCʱ��
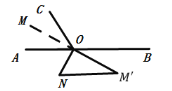
![]() ��
��
�����ǰ�MON��ʱ����ת��![]() 330������ת��
330������ת��![]() 22�룬
22�룬
����tΪ��4��16��10��22�룻
(3) �ߡ�MON=90������AOC=60����
����ת����ͼ��ON�ڡ�AOC���ⲿʱ��

���AOM=60��+��COM����NOC=90��+��COM��
���NOC -��AOM=30����
����ת����ͼ��ON�ڡ�AOC���ڲ�ʱ��
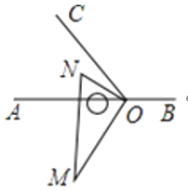
���AOM=90��-��AON����NOC=60��-��AON��
���AOM-��NOC=30����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�