题目内容
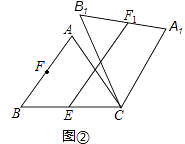
【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
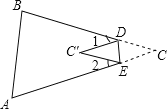
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
【答案】(1)![]() ;(2)2∠C=1+∠2.
;(2)2∠C=1+∠2.
【解析】
由折叠关系可得到∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,在再根据平角的性质,得到
∠C′DC+∠C′EC的值,在根据四边形的内角和为360°,即可求出∠C的度数;根据(1)问可知,∠C′DC+∠C′EC=360(∠1+∠2),2∠C==360°-(∠C′DC+∠C′EC),联立上式即可得到∠1、∠2、∠C三者之间的关系.
解:(1) ∵△C′DE是由△CDE折叠而成,
∴∠C=∠C′,∠C′DE=∠CDE,∠C′ED=∠CED,
又∠1+∠C′DC=180,∠2+∠C′EC=180
∴∠C′DC+∠C′EC=360(∠1+∠2)=290,
又∵四边形C′DCE的内角和为360,
∴∠C′+∠C=70,
∴∠C=35.
(2)根据(1)问可知,
∠C′DC+∠C′EC=360(∠1+∠2),
又∵四边形C′DCE的内角和为360,
2∠C==360°-(∠C′DC+∠C′EC),
联立上式即可得
2∠C=1+∠2,

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目