��Ŀ����
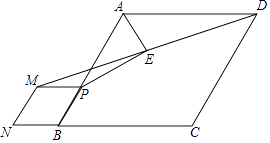
����Ŀ����ͼ��������y=ax2+3x��x���������ڵ�A��6��0��������ΪM���Գ���MB��x���ڵ�B������C��2��0��������CD��MB�ڵ�D��D��x���Ϸ�����OE��CD��MB�ڵ�E��EF��x�ύCD�ڵ�F����ֱ��MF��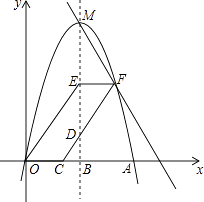
��1����a��ֵ��M�����ꣻ
��2����BDΪ��ֵʱ����Fǡ�����ڸ��������ϣ�
��3������DCB=45��ʱ��
����ֱ��MF�Ľ���ʽ��
���ӳ�OE��FM�ڵ�G���ı���DEGF���ı���OEDC������ֱ��ΪS1��S2 �� ��S1��S2��ֵΪ��ֱ��д�𰸣�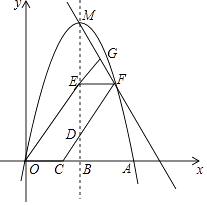
���𰸡�
��1���⣺��A��6��0������y=ax2+3x��36a+18=0�����a=�� ![]() ��
��
�����߽���ʽΪy=�� ![]() x2+3x��
x2+3x��
��y=�� ![]() ��x��3��2+
��x��3��2+ ![]() ��
��
��M���������3�� ![]() ��
��
��2���⣺��CF��OE��EF��OC��
���ı���OCFEΪƽ���ı��Σ�
��EF=OC=2��
�������ߵĶԳ���Ϊֱ��x=3��B��3��0����
��F��ĺ�����Ϊ5��
��x=5ʱ��y=�� ![]() x2+3x=
x2+3x= ![]() ����F��5��
����F��5�� ![]() ����
����
��BE= ![]() ��
��
��EF��BC��
���BCD�ס�EFD��
�� ![]() =
= ![]() =
= ![]() ��
��
��BD= ![]() BE=
BE= ![]() ��
�� ![]() =
= ![]() ��
��
����BDΪ ![]() ʱ����Fǡ�����ڸ���������
ʱ����Fǡ�����ڸ���������
��3����CD��OE,���BOE=��DCB=45����BOEΪ����ֱ��������, ��BE=OE=3,��E��3,3��,��ֱ��OE�Ľ���ʽΪy=x,ͬ���ɵá�BCDΪ����ֱ��������,��BD=BC=1,��DE=2,��EF��OC,EF=OC=2,��F��5,3��,��ֱ��MF�Ľ���ʽΪy=kx+b,��M��3,![]() ��,F��5,3�������
��,F��5,3�������  ,���
,���  ,��ֱ��MF�Ľ���ʽΪy=��
,��ֱ��MF�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��,
��,![]()
���������⣺��3���ڽⷽ����  ��
��  ����G��
����G�� ![]() ��
�� ![]() ����
����
��S1=S��GEF+S��DEF= ![]() ��2����
��2���� ![]() ��3��+
��3��+ ![]() ��2��2=
��2��2= ![]() ��
��
S2=S��BOE��S��BCD= ![]() ��3��3��
��3��3�� ![]() ��1��1=4��
��1��1=4��
�� ![]() =
= ![]() =
= ![]() ��
��
���Դ��� ![]() ��
��
�����㾫����������Ҫ������ȷ��һ�κ����ı���ʽ�Ͷ��κ�������ֵ�����֪ʶ�㣬��Ҫ����ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�