题目内容
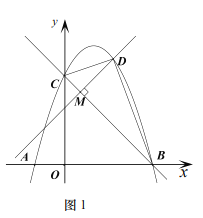
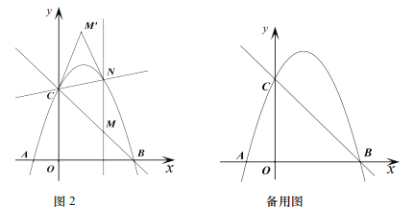
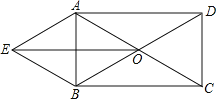
【题目】如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.
(1)求证:四边形AOBE是菱形;
(2)若∠EAO+∠DCO=180°,DC=3,求四边形ADOE的面积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1) 根据矩形的性质有OA=OB=OC=OD,根据四边形ADOE是平行四边形,得到OD∥AE,AE=OD. 等量代换得到AE=OB,即可证明四边形AOBE为平行四边形,根据有一组邻边相等的平行四边形是菱形即可证明;
(2)根据菱形的性质有∠EAB=∠BAO,根据矩形的性质有AB∥CD,根据平行线的性质有∠BAC=∠ACD,求出∠DCA=60°,求出AD=![]() ,根据面积公式SΔADC,即可求解.
,根据面积公式SΔADC,即可求解.
解:(1)∵四边形ABCD是矩形,
∴DO=BO.
∵四边形ADOE是平行四边形,
∴AE∥DO,AE=DO,AD∥OE.
∴AE∥BO,AE=BO.
∴四边形AOBE是平行四边形.
∵AD⊥AB,AD∥OE,
∴AB⊥OE.
∴四边形AOBE是菱形;
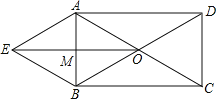
(2)设AB与EO交点为M.
∵AB∥CD,
∴∠DCO=∠BAO.
∵四边形AOBE是菱形,
∴∠EAO=2∠BAO.
∵∠EAO+∠DCO=180°,
∴∠BAO=120°,∠EAM=60°.
又AM=![]() AB=
AB=![]() ,
,
∴EM=![]() ,
,
∴EO=![]() ,
,
∴△AEO面积为![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴四边形ADOE面积=![]() .
.

练习册系列答案
相关题目