Question

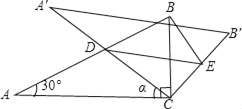
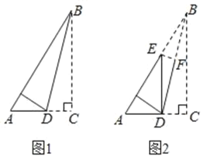
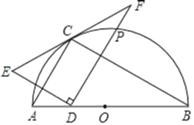
【题目】如图，在△ABC中，AB＝8，∠CBA＝30°，以AB为直径作半圆O，半圆O恰好经过点C，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．

（1）求证：CE＝CF

（2）填空：①若DF与半圆O相交于点P，则当点D与点O重合时，的长为　 　

②在点D的运动过程中，当EF与半圆O相切时，EF的长为　 　．

Answer 1

【答案】（1）见解析；（2）①；②4．

【解析】

（1）由点E与点D关于AC对称可得CE＝CD，再根据DF⊥DE即可证到CE＝CF；

（2）①根据已知条件得到DE⊥AC，推出DF⊥BC，得到∠FDB＝60°，根据弧长的公式即可得到结论；

②连接OC，CD，推出△AOC是等边三角形，根据切线的性质得到∠ACE＝∠B＝30°，得到∠OCD＝30°，根据三角函数的定义得到CD＝sin60°AC＝2，于是得到结论．

（1）连接CD，如图所示，

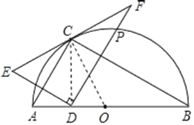
∵点E与点D关于AC对称，

∴CE＝CD，

∴∠E＝∠CDE，

∵DF⊥DE，

∴∠EDF＝90°，

∴∠E+∠F＝90°，∠CDE+∠CDF＝90°，

∴∠F＝∠CDF，

∴CD＝CF，

∴CE＝CD＝CF；

（2）①∵点E与点D关于AC对称，

∴DE⊥AC，

∵∠ACB＝∠EDF＝90°，

∴DF⊥BC，

∴∠FDB＝60°，

当点D与点O重合时，的长＝＝，

故答案为：；

②连接OC，CD，

∵∠CBA＝30°，

∴∠AOC＝60°，

∵OC＝OA，

∴△AOC是等边三角形，

∵EF与半圆O相切，

∴∠ACE＝∠B＝30°，

∴∠ACD＝30°，

∴∠ADC＝90°，

∴∠OCD＝30°，

∴CD＝sin60°AC＝2，

∵CE＝CD＝CF，

∴EF＝2CD＝4．

故答案为：4．