题目内容
【题目】我国的《洛书》中记载着世界上最古老幻方:将1-9这九个数字填入3×3的方格内,使三行、三列、两对角线上的三个数之和都相等.如图的幻方中字母m所能表示的所有数中最大的数是( )
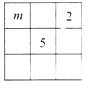
A.6B.7C.8D.9
【答案】A
【解析】
根据每行、每列、每条对角线上的三个数之和相等可分别用含m的代数式表示出其余的6个数,再根据这些数都是正整数列出不等式求解即可.
解:根据“每行、每列、每条对角线上的三个数之和相等”,可知三行、三列、两对角线上的三个数之和都等于15,
∴第一行第二个数为:15﹣2﹣m=13﹣m,
第三行第一个数为:15﹣2﹣5=8,
第三行第三个数为:15﹣5﹣m=10﹣m,
∴第二行第一个数为:15﹣8﹣m=7﹣m,
第二行第三个数为:15﹣2﹣(10﹣m)=3+m,
第三行第二个数为:15﹣8﹣(10﹣m)=m﹣3,
∵这九个数字都是正整数,
∴13﹣m>0,则m<13,
10﹣m>0,则m<10,
7﹣m>0,则m<7,
3+m>0,则m>﹣3,
m﹣3>0,则m>3,
∴m的取值范围是3<m<7,
又∵m为正整数,
∴m的最大整数值为6.
故选:A.

 名题金卷系列答案
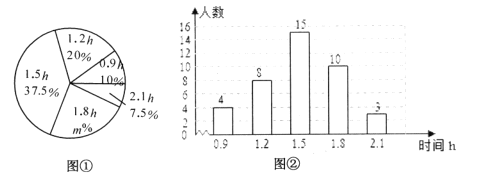
名题金卷系列答案【题目】某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别 | 时间/小时 | 频数/人数 |
A组 | 0≤ | 2 |
B组 | 1≤ | m |
C组 | 2≤ | 10 |
D组 | 3≤ | 12 |
E组 | 4≤ | 7 |
F组 |
| 4 |
扇形统计图
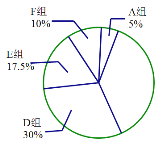
请根据图表中的信息解答下列问题:
(1)求频数分布表中的![]() 的值;
的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;
(3)已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿恰好都是男士的概率.