题目内容
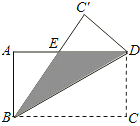
【题目】如图,矩形ABCD中,AB=3,BC=4,将该矩形沿对角线BD折叠,则图中阴影部分的面积为________.
【答案】![]()
【解析】
由矩形与折叠的性质,易证得△BDE是等腰三角形,然后设ED=EB=x,在Rt△ABE中,由AB2+AE2=BE2,可得方程:32+(4-x)2=x2,解此方程即可求得DE的长,继而求得阴影部分的面积.
∵四边形ABCD是矩形,
∴∠A=90°,AD∥BC,AD=BC=4,
∴∠EDB=∠DBC,
由折叠的性质可得:∠EBD=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
设ED=EB=x,则AE=AD-ED=4-x,
在Rt△ABE中,AB2+AE2=BE2,
即32+(4-x)2=x2,
解得:x=![]() ,
,
即DE=![]() ,
,
∴S阴影=S△BDE=![]() DEAB=
DEAB=![]() ×3=
×3=![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目