题目内容
【题目】在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上的一个动点,以AD为直角边向右作等腰Rt△ADF,使AD=AF,∠DAF=90°.
(1)如图1,连结CF,求证:△ABD≌△ACF;
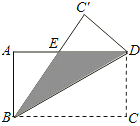
(2)如图2,过A点作△ADF的对称轴交BC于点E,猜想BD2,DE2,CE2关系,并证明你的结论;

【答案】(1)见解析;(2)CE2+BD2=DE2,理由见解析;
【解析】
(1)先判断出∠BAD=∠CAF.即可得出结论;
(2)利用△ABD≌△ACF,得出∠ACF=45°,BD=CF,进而得出∠DCF=90°,即可得出结论;
(1)∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
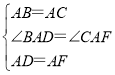 ,
,
∴△ABD≌△ACF;
(2)CE2+BD2=DE2;理由:
∵AB=AC,∠BAC=90°,
∴∠ABD=∠ACB=45°,
由(1)知,△ABD≌△ACF,
∴BD=CF,∠ACF=∠ABD=45°,
∴∠ECF=90°,
根据勾股定理得,CE2+CF2=EF2,
∵AE是△ADF的对称轴,
∴DE=EF,
∴CE2+BD2=DE2;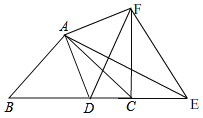

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目