题目内容
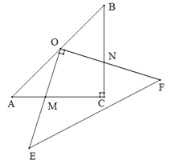
【题目】如图1,已知∠A+∠E+∠F+∠C=540°.

(1)试判断直线AB与CD的位置关系,并说明理由;
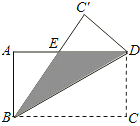
(2)如图2,∠PAB=3∠PAQ,∠PCD=3∠PCQ,试判断∠APC与∠AQC的数量关系,并说明理由.
【答案】(1)AB∥CD.理由见解析;(2)∠AQC=![]() ∠APC.理由见解析.
∠APC.理由见解析.
【解析】
(1)分别过点E、F作EM∥AB,FN∥AB,求出EM∥FN∥AB,根据平行线的性质和已知推出∠2+∠C=180°,根据平行线的判定得出即可;
(2)设∠PAQ=x,∠PCD=y,求出∠PAB=3x,∠BAQ=2x,∠PCD=3y,∠QCD=2y,过P作PG∥AB,过Q作QH∥AB,根据平行线的性质求出∠AQC=2x+2y=2(x+y),∠APC=3x+3y=3(x+y),即可得出答案.
解:(1)AB∥CD.理由如下:

分别过点E、F作EM∥AB,FN∥AB,
∵EM∥AB,FN∥AB,
∴EM∥FN∥AB,
∴∠1+∠A=180°,∠3+∠4=180°,
∵∠A+∠E+∠F+∠C=540°,
∴∠2+∠C=540°﹣180°﹣180°=180°,
∴FN∥CD,
∵FN∥AB,
∴AB∥CD;
(2)设∠PAQ=x,∠PCD=y,
∵∠PAB=3∠PAQ,∠PCD=3∠PCQ,
∴∠PAB=3x,∠BAQ=2x,
∠PCD=3y,∠QCD=2y,
过P作PG∥AB,过Q作QH∥AB,
∵AB∥CD,
∴AB∥CD∥PG∥GH,
∴∠AQH=∠BAQ=2x,∠QCD=∠CQH=2y,
∴∠AQC=2x+2y=2(x+y),
同理可得:∠APC=3x+3y=3(x+y),
∴![]() ,
,
即∠AQC=![]() ∠APC.
∠APC.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目