题目内容
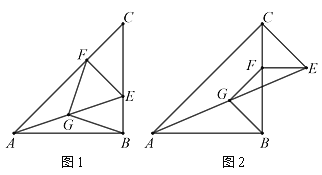
【题目】已知△ABC与△CEF均为等腰直角三角形,∠ABC=∠CFE=90°,连接AE,点G是AE中点,连接BG和GF.
(1)如图1,当△CEF中E、F落在BC、AC边上时,探究FG与BG的关系;
(2)如图2,当△CEF中F落在BC边上时,探究FG与BG的关系.
【答案】(1) FG=BG,FG⊥BG;证明见详解;(2)FG=BG,FG⊥BG;证明见详解;
【解析】
(1)由∠AFE=∠ABE=90°,点G是AE中点,则![]() ,
,![]() ,则得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
,则得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
(2)过点E作ED⊥AB,交AB延长线于点D,连接DG,CG,根据题意,找出相应的条件证明△GFE≌△GBD(SAS),得到FG=BG,与(1)证法一样,证明∠CGD=90°,通过等量代换即可得到∠FGB=90°.
解:(1)FG=BG,FG⊥BG;如图1,
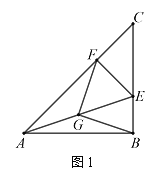
∵∠ABC=∠CFE=90°,
∴△ABE和△AFE是直角三角形,
∵点G是AE的中点,
∴![]() ,
,![]() ,
,
∴![]() .,∠GAF=∠GFA,∠GAB=∠GBA,
.,∠GAF=∠GFA,∠GAB=∠GBA,
∴∠FGE=2∠FAG,∠BGE=2∠BAG,
∵∠BAC=∠FAG+∠BAG=45°
∴∠BGF=∠FGE+∠BGE=2(∠FAG+∠BAG)=90°,
即FG⊥BG;
(2)![]() ,
,![]() ;
;
过点E作ED⊥AB,交AB延长线于点D,连接DG,CG,
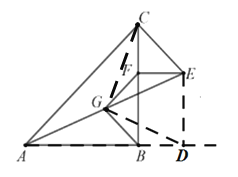
∵△ABC与△CEF均为等腰直角三角形,ED⊥AB,
∴∠FBD=∠BFE=∠EDB=90°,
∴四边形BFED是矩形,
∴BD=EF,
在直角三角形ADE和直角三角形ACE中,G是AE中点,
∴DG=GE=AG=CG=![]() ,
,
∴∠GED=∠GDE,
∴∠FEG=∠BDG,
∴△GFE≌△GBD(SAS),
∴GF=GB,CF=BD,
∵DG=AG=CG,
∴△CGF≌△DGB,∠CAG=∠ACG,∠DAG=∠ADG,
∴∠CGF=∠DGB,
∵∠CAG+∠DAG=45°,
∠CGE+∠DGE=2(∠CAG+∠DAG)=90°,
即∠CGD=90°,
∴∠CGD-∠CGF+∠DGB=∠FGB=90°,
即FG⊥BG.