题目内容
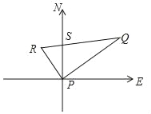
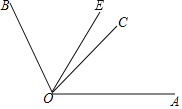
【题目】如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=![]() ∠AOE,求∠AOC的度数;
∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,则OB与OC有怎样的位置关系?为什么?
【答案】(1)36°;(2)OB⊥OC.
【解析】
(1)根据角平分线的定义和角的和差即可得到结论;
(2)根据角的和差和垂直的定义即可得到结论.
(1)∵∠COE=![]() ∠AOE,
∠AOE,
∴∠AOE=3∠COE,
∵OE是∠AOB的平分线,
∴∠AOB=2∠AOE=6∠COE,
∵∠AOB=180°,
∴∠COE=18°,
∴∠AOC=2∠COE=2×18°=36°;
(2)OB⊥OC,
设∠BOC=x°,则∠AOC=108°-x°,
∵∠BOC-∠AOC=72°,
∴x-(108-x)=72,
解得x=90,
∴∠BOC=90°,
∴OB⊥OC.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】如图,一条街道旁有A,B,C,D,E五幢居民楼,某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 | A | B | C | D | E |
大桶水/桶 | 38 | 55 | 50 | 72 | 85 |
他计划在这五幢楼中租赁一间门市房,设立大桶水供应点,若仅考虑这五幢楼内的居民取水所走路程之和最小,则可以选择的地点应在( ).
![]()
A. B楼 B. C楼 C. D楼 D. E楼