题目内容
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论。
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请求出凹四边形ABCE的面积.
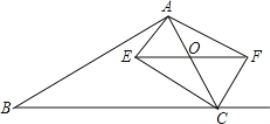
【答案】(1)证明见解析(2)当点O运动到AC的中点时,四边形CEAF是矩形(3)24
【解析】
(1)根据平行线的性质与等腰三角形的性质即可证明;(2)当点O运动到AC的中点时,四边形CEAF是矩形,由直角三角形斜边上的中线是斜边的一半即可证明;(3)利用凹四边形ABCE的面积=△ABC的面积△ACE的面积即可求解.
(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,
∵CE平分∠ACB,
∴∠BCE=∠OCE,
∴∠OEC=∠OCE,
∴EO=CO,
同理:FO=CO,
∴EO=FO;
(2)当点O运动到AC的中点时,四边形CEAF是矩形;理由如下:
由(1)得:EO=FO,
又∵O是AC的中点,
∴AO=CO,
∴四边形CEAF是平行四边形,
∵EO=FO=CO,
∴EO=FO=AO=CO,
∴EF=AC,
∴四边形CEAF是矩形;
(3)由(2)得:四边形CEAF是矩形,
∴∠AEC=90,
∴AC=AE2+EC2=5,
△ACE的面积=![]() AE×EC=
AE×EC=![]() ×3×4=6,
×3×4=6,
∵122+52=132,
即AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90,
∴△ABC的面积=![]() ABAC=
ABAC=![]() ×12×5=30,
×12×5=30,
∴凹四边形ABCE的面积=△ABC的面积△ACE的面积=306=24;

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?