题目内容
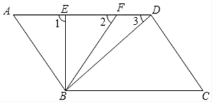
【题目】如图，已知AD∥BC，∠A＝∠C＝50°，线段AD上从左到右依次有两点E、F（不与A、D重合）
（1）AB与CD是什么位置关系，并说明理由；
（2）观察比较∠1、∠2、∠3的大小，并说明你的结论的正确性；
（3）若∠FBD：∠CBD＝1：4，BE平分∠ABF，且∠1＝∠BDC，求∠FBD的度数，判断BE与AD是何种位置关系？
【答案】（1）详见解析；（2）∠1＞∠2＞∠3，理由详见解析；（3）详见解析
【解析】
（1）根据AD∥BC，可得∠A+∠ABC＝180°，∠ABC＝130°， 则有∠C+∠ABC＝180°，可知AB∥CD；
（2）根据AD∥BC，得到∠1＝∠EBC，∠2＝∠FBC，∠3＝∠DBC，根据∠EBC＞∠FBC＞∠DBC，可得∠1＞∠2＞∠3；
（3）根据AD∥BC，AB∥CD，∠1＝∠EBC， ∠BDC＝∠ABD，根据∠1＝∠BDC，可得∠ABE＝∠DBC， 设∠FBD＝x°，则∠DBC＝4x°，有∠ABE＝∠EBF＝4x°，可列出4x+4x+x+4x＝130°，解得x＝10°，∠1＝90°，并可知BE⊥AD．
解：（1）AB∥CD，
∵AD∥BC，
∴∠A+∠ABC＝180°，
∵∠A＝50°，
∴∠ABC＝130°，
∵∠C＝50°，
∴∠C+∠ABC＝180°，
∴AB∥CD；
（2）∠1＞∠2＞∠3，
∵AD∥BC，
∴∠1＝∠EBC，∠2＝∠FBC，∠3＝∠DBC，
∵∠EBC＞∠FBC＞∠DBC，
∴∠1＞∠2＞∠3．
（3）∵AD∥BC，
∴∠1＝∠EBC，
∵AB∥CD，
∴∠BDC＝∠ABD，
∵∠1＝∠BDC，
∴∠ABD＝∠EBC
∴∠ABE＝∠DBC，
∵BE平分∠ABF，
设∠FBD＝x°，则∠DBC＝4x°，
∴∠ABE＝∠EBF＝4x°，
∴4x+4x+x+4x＝130°，
∴x＝10°，
∴∠1＝4x+x+4x＝90°，
∴BE⊥AD．
