题目内容
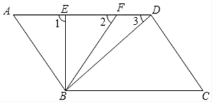
【题目】如图，在△ABC 中，点 D、E 分别在 BC、AC 上且 BD=CE，AD=DE， ∠C =∠ADE， 则∠B =∠C，试填写说理过程．
解因为∠EDB =∠C+∠DEC（ ）
即∠ADB+∠ADE =∠C+∠DEC
因为∠C =∠ADE（ ）
所以∠ =∠ （等式性质）
在△ABD 与△DCE 中，
所以△ABD ≌ △DCE（ ）
所以∠B =∠C（ ）
【答案】见详解
【解析】
利用三角形的外角等于不相邻的两个内角的和可证∠ADB=∠DEC．根据“SAS” 证得△ABD≌△DCE即可．
解：∵∠EDB =∠C＋∠DEC（三角形的外角性质）
即∠ADB＋∠ADE =∠C＋∠DEC
∵∠C =∠ADE（已知）
∴∠ADB =∠DEC（等式性质）
在△ABD 与△DCE 中，
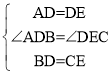
∴△ABD ≌ △DCE（SAS）
∴∠B =∠C（全等三角形的对应角相等）
练习册系列答案
相关题目
