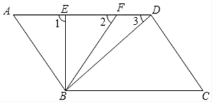
题目内容
【题目】已知在平面直角坐标系中,点O是坐标原点,A(﹣2,2),过A作AB⊥y轴于点B,以OB为边在第一象限内作△BCO.

(1)如图①,若△BCO为等边三角形,求点C坐标;
(2)如图②,若△BCO为以BO为斜边的直角三角形,求AC的最大值;
(3)如图③,若∠BCO=45°,BC=a,CO=b,请用a、b的代数式表示AC的长.
【答案】(1)点 C(![]() ,1);(2)AC的最大值为
,1);(2)AC的最大值为![]() +1;(3)AC=
+1;(3)AC=![]() .
.
【解析】
(1)过点C作CE⊥OB于点E,由等边三角形的性质可求BC=BO=CO=2,BE=EO=1,由勾股定理可求CE的长,即可求点C坐标;
(2)取BO中点E,连接AE,由勾股定理可求AE的长,由点C在以E为圆心,OE长为半径的圆上,即当点C在线段AC的延长线上时,AC有最大值,则可求AC的最大值;
(3)过点B作BF⊥OC于点F,过点C作CE⊥OB于点 E,CH⊥AB于H,由直角三角形的性质可求BF=CF=![]() BC=
BC=![]() a,由面积法可求CE的长,由勾股定理可求BE2,AC的值.
a,由面积法可求CE的长,由勾股定理可求BE2,AC的值.
解:(1)如图1,过点C作CE⊥OB于点E,
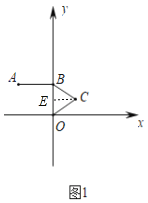
∵A(﹣2,2),过A作AB⊥y轴于点B,
∴点B(0,2),
∵△BCO是等边三角形,CE⊥BO,
∴BC=BO=CO=2,BE=EO=1,
∴CE=![]() ,
,
∴点 C(![]() ,1);
,1);
(2)如图2,取BO中点E,连接AE,
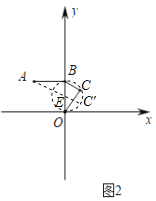
∵点E是BO中点,
∴OE=BE=1,
∴AE=![]() ,
,
∵△BCO为以BO为斜边的直角三角形,
∴点C在以E为圆心,OE长为半径的圆上,
∴当点C在线段AC的延长线上时,AC有最大值,
即AC的最大值为![]() +1;
+1;
(3)如图3,过点B作BF⊥OC于点F,过点C作CE⊥OB于点 E,CH⊥AB于H,
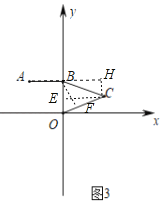
∵BF⊥OC,∠BCO=45°,
∴BF=CF=![]() BC=
BC=![]() a,
a,
∵S△OBC=![]() ×OB×EC=
×OB×EC=![]() ×OC×BF,
×OC×BF,
∴2EC=![]() ba,
ba,
∴EC=![]() ab,
ab,
∴BE2=BC2﹣EC2=a2﹣(![]() ab)2,
ab)2,
∵CH⊥AH,EC⊥OB,OB⊥BH,
∴四边形BHCE是矩形,
∴CH=BE,BH=EC,
∴AC2=AH2+CH2=(2+![]() ab)2+a2﹣(
ab)2+a2﹣(![]() ab)2=a2+
ab)2=a2+![]() ab+4
ab+4
∴AC=![]()