题目内容
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC=____.

【答案】![]()
【解析】
过A作AD⊥l3于D,过C作CE⊥l3于E,根据AAS证△DAB≌△EBC,求出BE=3,根据勾股定理求出AC.
过A作AD⊥l3于D,过C作CE⊥l3于E,则BF的长就是点B到AC的距离.
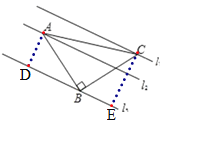
∵AD⊥l3,CE⊥l3,
∴∠ADB=∠ABC=∠CEB=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠DAB=∠CBE,
在△DAB和△EBC中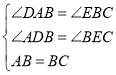 ,
,
∴△DAB≌△EBC(AAS),
∴AD=BE=2,
∵CE=2+1=3,
在△CEB中,由勾股定理得BC=![]() =
=![]() =
=![]() ,
,
在△ABC中,由勾股定理得AC=![]() =
=![]() .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20