题目内容
(6分)如图,在菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F.

小题1: (1)DE和BF相等吗?请说明理由;
小题2: (2)连接AF、BE,四边形AFBE是平行四边形吗?说明理由.

小题1: (1)DE和BF相等吗?请说明理由;
小题2: (2)连接AF、BE,四边形AFBE是平行四边形吗?说明理由.
小题1:(1)相等,连接BD,证明四边形DEFB是平行四边形,则BF=DE=AE
小题2:(2)是平行四边形,理由是AE平行且等于BF
分析:
(1)设AB、EF相交于G,连接BD,根据菱形的对角线互相垂直可得BD⊥AC,然后求出EG∥BD,判断出EG是△ABD的中位线,从而求出AG=BG,再根据两直线平行,内错角相等求出∠AEG=∠BFG,利用“角角边”证明△AEG和△BFG全等,根据全等三角形对应边相等可得AE=BF,从而求出DE=BF;
(2)根据一组对边平行且相等是四边形是平行四边形解答。
解答:

(1)DE=BF.理由如下:如图。
设AB、EF相交于G,连接BD,
在菱形ABCD中,BD⊥AC,
∵EF⊥AC,
∴EG∥BD,
∵E是AD中点,
∴EG是△ABD的中位线,
∴AG=BG,
又∵AD∥BC,
∴∠AEG=∠BFG,
在△AEG和△BFG中,∠AEG=∠BFG、∠AGE=∠BGF、AG=BG,
∴△AEG≌△BFG(AAS),
∴AE=BF,
∵E是AD中点,
∴AE=DE,
∴DE=BF。
(2)四边形AFBE是平行四边形。
理由如下:
∵四边形ABCD是菱形,
∴AD∥BC,
∴AE∥BF,
又∵AE=BF,
∴四边形AFBE是平行四边形。
点评:本题考查了菱形的性质,平行四边形的判定,全等三角形的判定与性质,主要利用了菱形的对角线互相垂直的性质,作辅助线构造出全等三角形的是解题的关键,也是本题的难点。

练习册系列答案
相关题目

 的外侧作等边
的外侧作等边 ,则
,则 的度数为( )
的度数为( )





 、
、 、
、 分别是等边
分别是等边 的边BC、CA、AB的中点,在图2中,
的边BC、CA、AB的中点,在图2中, 、
、 、
、 分别是
分别是 的边
的边 、
、 、
、 的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
的中点,……,按此规律,则第n个图形中菱形的个数共有( )个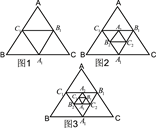
 B.
B.  C.
C.  D.
D. 
