题目内容
如图,在图1中, 、
、 、
、 分别是等边
分别是等边 的边BC、CA、AB的中点,在图2中,
的边BC、CA、AB的中点,在图2中, 、
、 、
、 分别是
分别是 的边
的边 、
、 、
、 的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
A. B.
B.  C.
C.  D.
D. 
 、
、 、
、 分别是等边
分别是等边 的边BC、CA、AB的中点,在图2中,
的边BC、CA、AB的中点,在图2中, 、
、 、
、 分别是
分别是 的边
的边 、
、 、
、 的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
的中点,……,按此规律,则第n个图形中菱形的个数共有( )个
A.
 B.
B.  C.
C.  D.
D. 
C
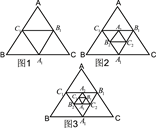
析:根据菱形的判断定理:四条边相等的四边形是菱形或邻边相等的平行四边形是菱形.在图(1)中,有3个菱形;在图(2)中,有6个菱形;…按此规律,则第n个图形中菱形的个数共有3n个.
解答:解:在图(1)中,A1、B1、C1分别是等边三角形△ABC的边BC、CA、AB的中点,
∴A1C1∥AB1A1B1∥BC1A1C1∥B1C
∵A1C1=AB=1A1B1=BC1=A1C1=B1C,
∴四边形A1B1AC1、A1B1C1B、A1C1B1C是菱形,共有3个.
在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
同理可证:四边形A1B1AC1、A1B1C1B、A1C1B1C、A2B2C2B1、A2B2A1C2、A2C2B2C1是菱形,共有6个.
…
按此规律,则第n个图形中菱形的个数共有3n个.
故选C.
解答:解:在图(1)中,A1、B1、C1分别是等边三角形△ABC的边BC、CA、AB的中点,
∴A1C1∥AB1A1B1∥BC1A1C1∥B1C
∵A1C1=AB=1A1B1=BC1=A1C1=B1C,
∴四边形A1B1AC1、A1B1C1B、A1C1B1C是菱形,共有3个.
在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
同理可证:四边形A1B1AC1、A1B1C1B、A1C1B1C、A2B2C2B1、A2B2A1C2、A2C2B2C1是菱形,共有6个.
…
按此规律,则第n个图形中菱形的个数共有3n个.
故选C.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 为正方形
为正方形 的对角线,
的对角线, 为
为 ,
, ,当
,当 时,
时, 的度数为( )
的度数为( )






