Question

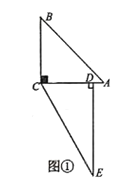
【题目】如图，四边形ABCD是平行四边形，AD＝AC，AD⊥AC，E是AB的中点，F是AC延长线上一点．

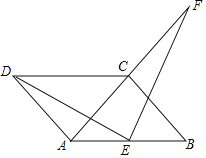
（1）若ED⊥EF，求证：ED＝EF；

（2）在（1）的条件下，若DC的延长线与FB交于点P，试判定四边形ACPE是否为平行四边形？并证明你的结论（请先补全图形，再解答）．

Answer 1

【答案】（1）见解析；（2）四边形ACPE为平行四边形，理由见解析

【解析】

（1）连接CE，根据全等三角形的判定和性质即可得到结论；

（2）根据全等三角形的性质得到CF＝AD，等量代换得到AC＝CF，于是得到CP＝AB＝AE，根据平行四边形的判定定理即可得到四边形ACPE为平行四边形．

（1）证明：在ABCD中，∵AD＝AC，AD⊥AC，

∴AC＝BC，AC⊥BC，

连接CE，如图所示：

∵E是AB的中点，

∴AE＝EC，CE⊥AB，

∴∠ACE＝∠BCE＝45°，

∴∠ECF＝∠EAD＝135°，

∵ED⊥EF，

∴∠CEF＝∠AED＝90°﹣∠CED，

在△CEF和△AED中，，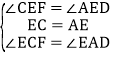

∴△CEF≌△AED（ASA），

∴ED＝EF；

（2）四边形ACPE为平行四边形，理由如下：

由（1）知△CEF≌△AED，CF＝AD，

∵AD＝AC，

∴AC＝CF，

∵DP∥AB，

∴FP＝PB，

∴CP＝AB＝AE，

∴四边形ACPE为平行四边形．