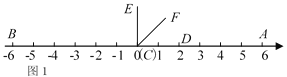题目内容
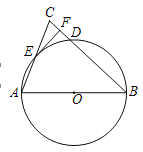
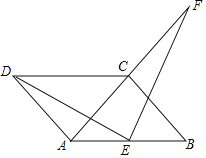
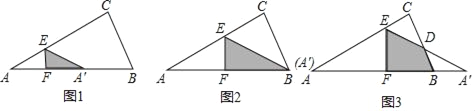
【题目】已知:如图1,△ABC中,AB=6,AC=![]() ,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
,BC=3,过边AC上的动点E(点E不与点A、C重合)作EF⊥AB于点F,将△AEF沿EF所在的直线折叠得到△A'EF,设CE=x,折叠后的△A'EF与四边形BCEF重叠部分的面积记为S.
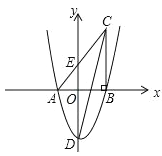
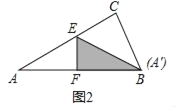
(1)如图2,当点A'与顶点B重合时,求AE的长;
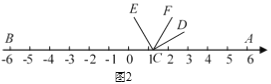
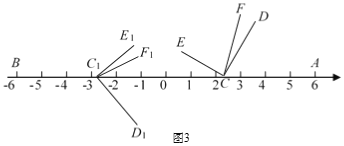
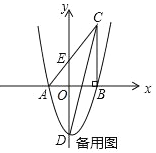
(2)如图3,当点A'落在△ABC的外部时,A'E与BC相交于点D,求证:△A'BD是等腰三角形;
(3)试用含x的式子表示S,并求S的最大值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)首先证明∠A=30°,在Rt△AEF中,解直角三角形即可解决问题;
(2)想办法证明∠A′=∠A′DB=30°,可得BD=BA′;
(3)分两种情形分别求解,①如图3中,当0<x≤![]() 时,重叠部分是四边形EFBD.②如图1中,
时,重叠部分是四边形EFBD.②如图1中,![]() <x<3
<x<3![]() 时,重叠部分是△EFA′;
时,重叠部分是△EFA′;
(1)如图2中,
∵AC2+BC2=(3![]() )2+32=36,AB2=36,
)2+32=36,AB2=36,
∴△ABC是直角三角形,∠C=90°,
当点A'与顶点B重合时,AF=FB=3,
cosA=![]() ,
,
∴∠A=30°,
∴AE=![]() .
.
(2)如图3中,
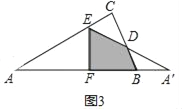
由(1)可知∠A=30°,∠C=90°,
∴∠ABC=60°,
∵∠ABC=∠A′+∠BDA′,∠A′=∠A=30°,
∴∠A′=∠A′DB=30°,
∴BD=BA′,
∴△BDA′是等腰三角形.
(3)①如图3中,当0<x≤![]() 时,重叠部分是四边形EFBD,
时,重叠部分是四边形EFBD,
S=S△EFA′﹣S△BDA′
=![]()
![]() (3
(3![]() ﹣x)
﹣x)![]() (3
(3![]() ﹣x)﹣
﹣x)﹣![]() [
[![]() (3
(3![]() ﹣x)﹣6]×
﹣x)﹣6]×![]() [
[![]() (3
(3![]() ﹣x)﹣6]
﹣x)﹣6]
=﹣![]()
∴S最大值=
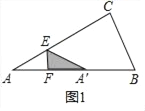
②如图1中,![]() <x<3
<x<3![]() 时,重叠部分是△EFA′,
时,重叠部分是△EFA′,
S=![]() (x﹣3
(x﹣3![]() )2,
)2,
S最大值=3![]() ,
,
3![]() <
<![]() ,
,
∴S的最大值为![]() .
.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.