题目内容
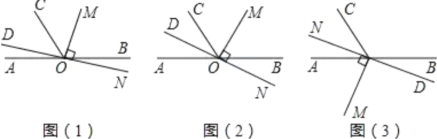
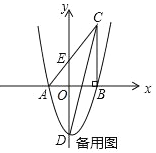
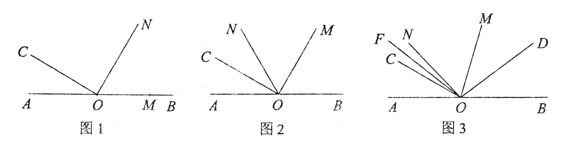
【题目】如图1, 点![]() 在直线
在直线![]() 上,
上,![]() ,将.
,将.![]() 绕着点
绕着点![]() 以
以![]() 的速度逆时针旋转,设旋转时间为
的速度逆时针旋转,设旋转时间为![]() .
.
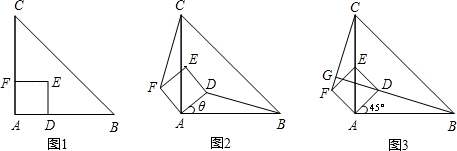
(1)如图2,当![]() 平分
平分![]() 时,
时,![]() ______
______![]() ; 图中
; 图中![]() 的补角有: ______;
的补角有: ______;
(2)如图3,当![]() 时,
时,![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(3)在![]() 绕着点
绕着点![]() 逆时针旋转的过程中,当
逆时针旋转的过程中,当![]() ______
______![]() 时,
时,![]() .
.
【答案】(1)![]() ; 图中
; 图中![]() 的补角有:
的补角有: ![]() 和
和![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]()
【解析】
(1)根据角平分线的性质求出∠AON的度数,进而求出∠BON和∠BOM的度数,再根据“时间=路程÷速度”,即可得出答案;根据补角的定义即可得出答案;
(2)先设出∠BOM和∠CON的度数,再根据角平分线的定义求出∠NOF和∠DOM的度数,即可得出答案;
(3)分情况进行讨论,①当ON位于直线AB上方,OM位于∠BOC中时;②当ON位于直线AB下方,OM位于∠AOC中时;③OM和ON均位于直线AB下方时;④当ON位于直线AB上方,OM位于直线AB下方时;分别求出每种情况下∠AON和∠COM的度数,再令∠AON=∠COM,解方程即可得出答案.
解:(1)当OC平分∠AON时,∠AON=2∠AOC=60°
∴∠BON=120°
又∠MON=60°
∴∠BOM=∠BON-∠MON=60°
∴t=60÷10=6(s);
图中![]() 的补角有:
的补角有:![]() 和
和![]() ;
;
(2) ∵运动时间为![]() 秒,运动速度为
秒,运动速度为![]() ,则
,则
![]()
又∵![]() 平分
平分![]() ,
,![]() 平分
平分![]()
∴![]() ,
,
![]()
∴![]()
∴当![]() 时,
时,![]() 的度数为
的度数为![]()
(3)①当ON位于直线AB上方,OM位于∠BOC中时
∠AON=(120-10t)°,∠COM=(150-10t)°
又∠AON=∠COM,即(120-10t)°=(150-10t)°,无解;
②当ON位于直线AB下方,OM位于∠AOC中时
∠COM=(150-10t)°,∠AON=(10t-120)°
又∠AON=∠COM,即(150-10t)°=(10t-120)°,解得t=13.5;
③OM和ON均位于直线AB下方时
∠COM=(10t-150)°,∠AON=(10t-120)°
又∠AON=∠COM,即(10t-150)°=(10t-120)°,无解;
④当ON位于直线AB上方,OM位于直线AB下方时
∠COM=(10t-150)°,∠AON=(480-10t)°
又∠AON=∠COM,即(10t-150)°=(480-10t)°,解得t=31.5;
∴当![]() 或
或![]() 时,
时,![]()

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.