Question

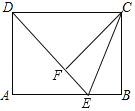
【题目】如图，矩形ABCD中，AB＝4，AD＝3，E是边AB上一点，将△CBE沿直线CE对折，得到△CFE，连接DF．

（1）当D、E、F三点共线时，证明：DE＝CD；

（2）当BE＝1时，求△CDF的面积；

（3）若射线DF交线段AB于点P，求BP的最大值．

Answer 1

【答案】（1）见解析；（2）；（3）4﹣

【解析】

（1）由矩形和折叠的性质可得∠DCE＝∠CEB＝∠FEC，即可证DE＝CD；

（2）延长EF交CD的延长线于点G，由矩形和折叠的性质可证GE＝GC，由勾股定理可求CG＝5，即可求△CDF的面积；

（3）过点C作CH⊥DP于点H，连接CP，由相似三角形的性质可得＝，即当点H与点F重合时，CH最大，DH最小，AP最小，BP最大，由勾股定理可求AP的长，即可求BP的最大值．

证明：（1）∵四边形ABCD是矩形

∴AB＝CD＝4，AD＝BC＝3，AB∥CD，

∴∠DCE＝∠CEB

∵△CBE翻折得到△CFE

∴∠FEC＝∠CEB

∴∠DCE＝∠FEC

∴DE＝CD

（2）如图1，延长EF交CD的延长线于点G，

∵四边形ABCD是矩形

∴AB＝CD＝4，AD＝BC＝3，AB∥CD，

∴∠DCE＝∠CEB

∵△CBE翻折得到△CFE

∴∠FEC＝CEB，CF＝BC＝3，EF＝BE＝1，∠CFE＝90°

∴∠DCE＝∠FEC，∠CFG＝90°

∴CG＝EG，

∴GF＝GE﹣EF＝CG﹣1

∵在Rt△CGF中，CG2＝CF2+GF2，

∴CG2＝9+（CG﹣1）2，

解得：CG＝5

∵△CDF与△CGF分别以CD、CG为底时，高相等

∴

∴S△CDF＝S△CGF＝＝

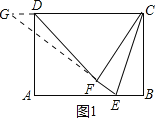
（3）如图2，过点C作CH⊥DP于点H，连接CP，

∵CD∥AB

∴∠CDP＝∠APD，且∠A＝∠CHD＝90°

∴△ADP∽△HCD

∴＝，

∵CH≤CF，CF＝BC＝AD＝3

∴CH≤3

∴当点H与点F重合时，

CH最大，DH最小，AP最小，BP最大，

此时，在△ADP与△HCD

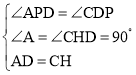
∴△ADP≌△HCD（AAS）

∴CD＝DP＝4，AP＝DF

∵AP＝＝

∴BP的最大值为4﹣．