Question

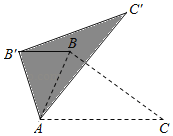
【题目】如图（1），在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝，AB与CE交于F，ED与AB、BC分别交于M、H．

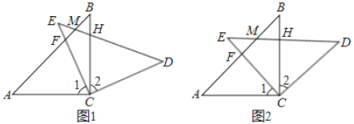
（1）求证：CF＝CH；

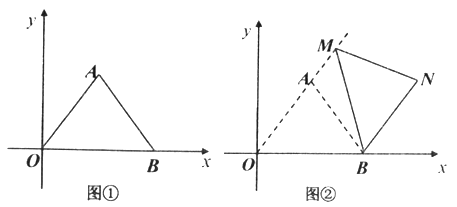
（2）如图（2），△ABC不动，将△EDC绕点C旋转到∠BCE=时，试判断四边形ACDM是什么四边形？并证明你的结论．

Answer 1

【答案】（1）见解析；（2）菱形，理由见解析

【解析】

（1）要证明CF=CH，可先证明△BCF≌△ECH，由∠ABC=∠DCE=90°，AC=CE=CB=CD，可得∠B=∠E=45°，得出CF=CH；
（2）当旋转角∠BCD=45°，推出四边形ACDM是平行四边形，由AC=CD判断出四边形ACDM是菱形．

（1）∵AC=CE=CB=CD，∠ACB=∠ECD=90°，
∴∠A=∠B=∠D=∠E=45°，
在△BCF和△ECH中，

∵,

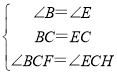∴△BCF≌△ECH（ASA），
∴CF=CH；
（2）∠BCE=45°时，四边形ACDM是菱形，

理由如下：

∵∠ACB=∠DCE=90°，∠BCE=45°，
∴∠ACE=∠DCB=45°．
∵∠E=45°，
∴∠ACE =∠E，
∴AC∥DE，
∴∠AMH=180°-∠A=135°，
又∵∠A=∠D=45°，

∴∠AMH+∠D=135°+45°=180，

∴AM∥CD，
∴四边形ACDM是平行四边形；
∵AC=CD，
∴四边形ACDM是菱形．