Question

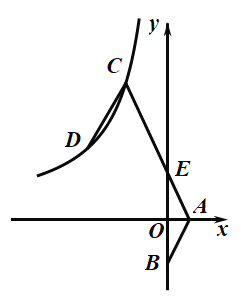
【题目】如图，在平面直角坐标系中，将线段平移得到线段当时，点同时落在反比例函数的图象上，则的值为_______．

Answer 1

【答案】

【解析】

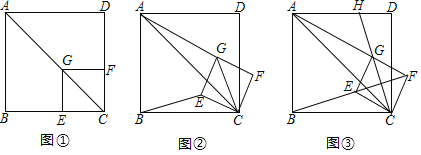
作出如图的辅助线，证得△CDH△BAO，四边形DGFH为矩形，得到FO=2，设点C的坐标为(-2，b)，则点D的坐标为(-3，b-2)，利用反比例函数图像上点的坐标特征即可求解．

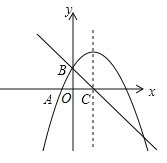
分别过点C、D作轴的垂线，垂足为G、F，作DH⊥CF于H，如图：

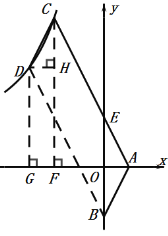
根据平移的性质，知：四边形ABDC为平行四边形，

∴△CDH△BAO，四边形DGFH为矩形，

∵EO∥CF，，

∴，

∵A(1，0)，B(0，-2)，

∴AO=DH=GF=1，BO=CH=2，

∴AF=3AO=3，

∴FO=2，

设点C的坐标为(-2，b)，则点D的坐标为(-3，b-2)，

∵点C、点D都在反比例函数的图象上，

∴，

解得：，，

故答案为：．