题目内容
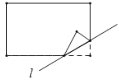
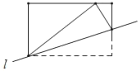
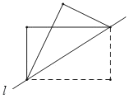
【题目】如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.
(1)求证:∠DOC=2∠G.
(2)已知⊙O的半径为3.
①若BE=2,则DA= .
②当BE= 时,四边形DOCF为菱形.

【答案】(1)见解析;(2)①![]() ;②3.
;②3.
【解析】
(1)根据切线的性质可得∠ODB=90°,再根据平行线的判定可得OD∥CG,进而得到∠G=∠ODE,因为OD=OE,所以∠OED=∠ODE,最好根据圆周角为圆心角的一半即可得证;
(2)①利用勾股定理求得BD=4,由(1)知,OD∥CG,可得△BOD∽△BCA,再根据相似三角形的的性质求解即可;
②如图,连接DF,OF,根据菱形的性质可得DF=CF=OC=OD=3,进而可得△ODF为等边三角形,即∠ODF=60°,根据30°角所对直角边为斜边的一半可得AF=![]() ,进而可得AC=
,进而可得AC=![]() ,由(2)知△BOD∽△BCA,再根据相似三角形的的性质求解即可.
,由(2)知△BOD∽△BCA,再根据相似三角形的的性质求解即可.
(1)证明:∵AB为⊙O的切线,
∴OD⊥AB,
∴∠ODB=90°,
∴∠BAC=∠ODB=90°,
∴OD∥CG,
∴∠G=∠ODE,
∵OD=OE,
∴∠OED=∠ODE,
∵∠DOC=∠ODE+∠OED,
∴∠DOC=2∠ODE=2∠G;
(2)解:①在Rt△BOD中,
OD=3,OB=OE+BE=5,
∴BD=![]() =4,
=4,
由(1)知,OD∥CG,
∴△BOD∽△BCA,
∴![]() ,
,
即![]() ,
,
∴AD=![]() ,
,
故答案为:![]() ;
;
②如下图,连接DF,OF,
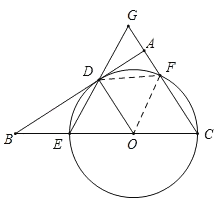
当四边形DOCF为菱形时,
DF=CF=OC=OD=3,
∵OF=3,
∴△ODF为等边三角形,
∴∠ODF=60°,
∴∠ADF=90°﹣∠ODF=30°,
在Rt△DAF中,DF=3,
∴AF=3×![]() =
=![]() ,
,
∴AC=CF+AF=![]() ,
,
由(2)知,∴△BOD∽△BCA,
∴![]() ,
,
即 ,
,
∴BE=3,
故答案为:3.

【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
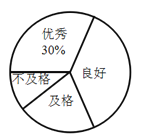
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.