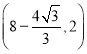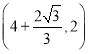题目内容
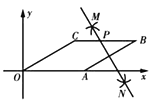
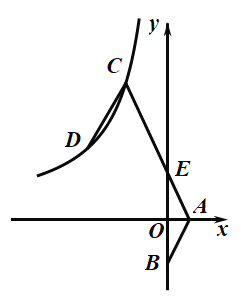
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,图像的对称轴交
,图像的对称轴交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求二次函数的解析式![]() 和一次函数的解析式
和一次函数的解析式![]() ;
;
(2)点![]() 在
在![]() 轴下方的二次函数图像上,且
轴下方的二次函数图像上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)结合图像,求当![]() 取什么范围的值时,有
取什么范围的值时,有![]() .
.
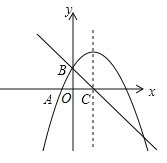
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 和
和![]() ;(3)当
;(3)当![]() 或
或![]() 时,有
时,有![]() .
.
【解析】
(1)将A、B代入抛物线,可求得二次函数解析式,然后求出点C的坐标,根据B、C的坐标,求出直线的解析式;
(2)设点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,根据△ACP的大小,可求出h的值,从而得出点P的坐标;
,根据△ACP的大小,可求出h的值,从而得出点P的坐标;
(3)联立抛物线和直线解析式,求出交点坐标,根据图像可得出不等式的解集.
(1)将点![]() 和点
和点![]() 代入
代入![]()

解得:![]()
![]() 二次函数的解析式
二次函数的解析式![]()
![]() 二次函数的对称轴为直线
二次函数的对称轴为直线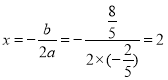
![]()
将点![]() 和点
和点![]() 代入
代入![]()
![]()
解得:![]()
![]() 一次函数的解析式
一次函数的解析式![]()
(2)设点![]() 到
到![]() 轴的距离为
轴的距离为![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 在
在![]() 轴下方
轴下方
![]() 点
点![]() 的纵坐标为-22
的纵坐标为-22
将![]() 代入
代入![]()
![]()
解得:![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 和
和![]() .
.
(3)联立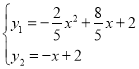
解得:![]() 或
或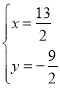 .
.
![]() 抛物线与直线的交点为
抛物线与直线的交点为![]() 和
和![]()
由图像可知,当![]() 或
或![]() 时,有
时,有![]() .
.

练习册系列答案
相关题目