题目内容
【题目】符合下列条件之一的四边形不一定是菱形的是( )
A. 四条边相等
B. 两组邻边分别相等
C. 对角线相互垂直平分
D. 两条对角线分别平分一组对角
【答案】B
【解析】
根据菱形的判定定理即可判断A;举出反例图形即可判断B;根据线段垂直平分线定理推出AB=AD,BC=CD,AB=BC,推出AB=BC=CD=AD,根据菱形的判定推出即可判断C;求出四边形ABCD是平行四边形,推出即可判断D.
A、∵AB=BC=CD=AD,
∴四边形ABCD是菱形,正确,故本选项错误;
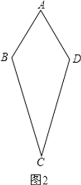
B、根据AB=AD,BC=CD,不能推出四边形ABCD是菱形,如图2,
错误,故本选项正确;
C、如图1, ∵AC⊥BD,OD=OB,
∴AB=AD,BC=CD,
∵BD⊥AC,AO=CO,
∴AB=BC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,正确,故本选项错误;
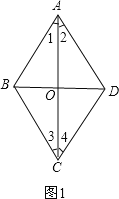
D、如图1, ∵AC平分∠BAD和∠BCD,
∴∠1=∠2, ∠3=∠4,
∵∠1+∠3+∠ABC=180°, ∠2+∠4+∠ADC=1880°,
∴∠ABC=∠ADC,
同理可证∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴AB=BC,
∴平行四边形ABCD是菱形,正确,故本选项错误.
故选B.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目





