题目内容
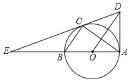
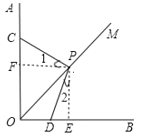
【题目】已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证:PC=PD.

【答案】见解析
【解析】
过P分别作PE⊥OB于E,PF⊥OA于F,由角平分线的性质易得PE=PF,然后由同角的余角相等证明∠1=∠2,即可由ASA证明△CFP≌△DEP,从而得证.
证明:过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠1+∠FPD=90°
又∵∠AOB=90°
∴∠FPE=90°,
∴∠2+∠FPD=90°
∴∠1=∠2,
∵在△CFP和△DEP中: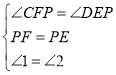 ,
,
∴△CFP≌△DEP(ASA)
∴PC=PD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目