题目内容
【题目】在菱形ABCD中,∠ABC=60°
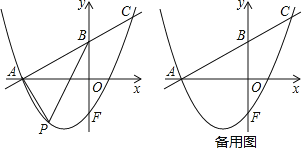
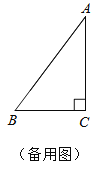
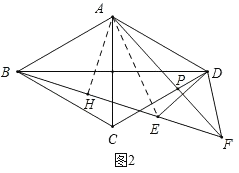
(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.
①求证:CE⊥AD;
②若AB=![]() ,BE=
,BE=![]() ,求AE的长;
,求AE的长;
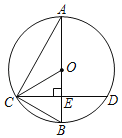
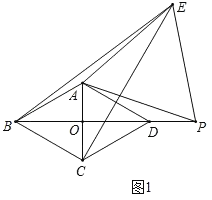
(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.

【答案】(1)①证明见解析;②AE=![]() ;(2)△ADF的面积为
;(2)△ADF的面积为![]() .
.
【解析】
(1)①证△ADC和△ABC是等边三角形,再证△BAP≌△CAE,推出∠ACE=30°,由∠ACE+∠CAD=90°即可证明结论;
②如图1,设AC与BD交于点O,证∠BCE=90°,由勾股定理求出CE,BP的长,由锐角三角函数等分别求出OA,OP的长,由勾股定理即可求出AP的长,即AE的长;
(2)如图2,连接AE,过点A作AH⊥BF于点H,证∠HAF=![]() ∠BAD=60°,再证△DEF为等边三角形,即可求出HF,AH的长,进一步求出△AEF的面积,证△ADF≌△AEF即可.
∠BAD=60°,再证△DEF为等边三角形,即可求出HF,AH的长,进一步求出△AEF的面积,证△ADF≌△AEF即可.
证明: (1)①在菱形ABCD中,∠ABC=60°,
∴∠ADC=60°,且AB=BC=DA=DC,
∴△ADC和△ABC是等边三角形,
∴AB=AC,∠BAC=∠CAD=60°,
又∵△APE是等边三角形,
∴AE=AP,∠EAP=60°,
∴∠BAC+∠CAP=∠PAE+∠CAP,
即∠BAP=∠CAE,
∴△BAP≌△CAE(SAS),
∴∠ACE=∠ABP=![]() ∠ABC=30°,
∠ABC=30°,
∵∠CAD=60°,
∴∠ACE+∠CAD=90°,
∴CE⊥AD;
②解:如图1,设AC与BD交于点O,
由①知,∠ACE=30°,且∠ACB=60°,
∴∠ACE+∠ACB=∠BCE=90°,
∵在Rt△BCE中,BC=AB=![]() ,BE=
,BE=![]() ,
,
∴CE=![]() =4,
=4,
由①知,△BAP≌△CAE,
∴BP=CE=4,
在Rt△BOC中,∠ACB=60°,
∴BO=![]() BC=
BC=![]() ,CO=AO=
,CO=AO=![]() BC=
BC=![]() ,
,
∴OP=BP﹣BO=![]() ,
,
∴在Rt△AOP中,
AP=![]() =
=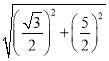 =
=![]() ,
,
∴AE=AP=![]() ;
;
(2)解:如图2,连接AE,过点A作AH⊥BF于点H,
∵点D关于AP的对称点为E,
∴AP垂直平分DE,
∴AD=AE,FD=FE,
∴∠EAF=∠DAF=![]() ∠EAD,∠DFA=∠EFA=
∠EAD,∠DFA=∠EFA=![]() ∠DFE,
∠DFE,
又∵在菱形ABCD中,AB=AD,
∴AB=AE,
∴AH垂直平分BE,
∴EH=BH=![]() BE=
BE=![]() ,∠BAH=∠EAH=
,∠BAH=∠EAH=![]() ∠BAE,
∠BAE,
∴∠HAF=∠EAH+∠EAF=![]() ∠BAD,
∠BAD,
∵∠ABC=60°,
∴∠BAD=180°﹣∠ABC=120°,
∴∠HAF=60°,
∴∠AFH=90°﹣∠HAF=30°,
∴∠DFE=60°,
∴△DEF为等边三角形,
∴EF=DE=5,
∴HF=HE+EF=![]() +5=
+5=![]() ,
,
在Rt△AHF中,∠AFH=30°,
∴AH=![]() HF=
HF=![]() ,
,
∴S△AEF=![]() EFAH=
EFAH=![]() ×5×
×5×![]() =
=![]() ,
,
∵AD=AE,FD=FE,AF=AF,
∴△ADF≌△AEF(SSS),
∴△ADF的面积为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.