题目内容
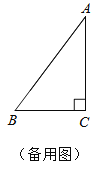
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.动点P,Q从点A同时出发,点P沿AB向终点B运动;点Q沿AC→CB向终点B运动,速度都是1cm/s.当一个点到达终点时,另一个点同时停止运动.设点P运动的时间为t(s),在运动过程中,点P,点Q经过的路线与线段PQ围成的图形面积为S(cm2).
(1)AC=_________cm;
(2)当点P到达终点时,BQ=_______cm;
(3)①当t=5时,s=_________;
②当t=9时,s=_________;
(4)求S与t之间的函数解析式.
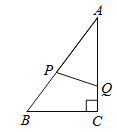
【答案】(1)8;(2)4;(3)①![]() ,②22;(4)
,②22;(4)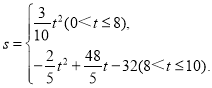
【解析】
(1)根据勾股定理求解即可;
(2)先求出点P到达中点所需时间,则可知点Q运动路程,易得CQ长,![]() ;
;
(3)①作PD⊥AC于D,可证△APD∽△ABC,利用相似三角形的性质可得PD长,根据面积公式求解即可;
②作PE⊥AC于E,可证△PBE∽△ABC,利用相似三角形的性质可得PE长,用![]() 可得s的值;
可得s的值;
(4)当0<t≤8时,作PD⊥AC于D,可证△APD∽△ABC,可用含t的式子表示出PD的长,利用三角形面积公式可得s与t之间的函数解析式;当8<t≤10时,作PE⊥AC于E,可证△PBE∽△ABC,利用相似三角形的性质可用含t的式子表示出PE长,用![]() 可得s与t之间的函数解析式.
可得s与t之间的函数解析式.
解:
(1)在Rt△ABC中,由勾股定理得![]()
![]()
(2)设点P运动到终点所需的时间为t,路程为AB=10cm,则![]()
![]() 点Q运动的路程为10cm,即
点Q运动的路程为10cm,即![]()
![]()
![]() cm
cm
所以当点P到达终点时,BQ=4cm.
(3)①作PD⊥AC于D ,则![]()
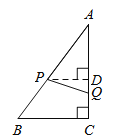
∵∠A=∠A.∠ADP=∠C=90°,
∴△APD∽△ABC.
∴![]() .
.
即![]()
∴![]() .
.
∴![]() .
.
②如图,作PE⊥AC于E,则![]()

∵∠B=∠B.∠BEP=∠C=90°,
∴△PBE∽△ABC.
∴![]() .
.
即![]() .
.
∴![]() .
.
∴![]()
![]() .
.
(4)当0<t≤8时,如图①.

作PD⊥AC于D.
∵∠A=∠A.∠ADP=∠C=90°,
∴△APD∽△ABC.
∴![]() .
.
即![]() .
.
∴![]() .
.
∴![]() .
.
当8<t≤10时,如图②.

作PE⊥AC于E.
∵∠B=∠B.∠BEP=∠C=90°,
∴△PBE∽△ABC.
∴![]() .
.
即![]() .
.
∴![]() .
.
∴![]()
![]() .
.
综上所述:

 同步轻松练习系列答案
同步轻松练习系列答案