题目内容
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
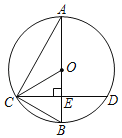
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
【答案】(1)见解析;(2)169π(cm2).
【解析】
(1)根据垂径定理,即可得![]() =
=![]() ,根据同弧所对的圆周角相等,证出∠BAC=∠BCD,再根据等边对等角,即可得到∠BAC=∠ACO,从而证出∠ACO=∠BCD;
,根据同弧所对的圆周角相等,证出∠BAC=∠BCD,再根据等边对等角,即可得到∠BAC=∠ACO,从而证出∠ACO=∠BCD;
(2)根据垂径定理和勾股定理列出方程,求出圆的半径,即可求出圆的面积.
解:(1)∵AB为⊙O的直径,AB⊥CD,
∴![]() =
=![]() .
.
∴∠BAC=∠BCD.
∵OA=OC,
∴∠BAC=∠ACO.
∴∠ACO=∠BCD;
(2)∵AB为⊙O的直径,AB⊥CD,
∴CE=![]() CD=
CD=![]() ×24=12(cm).
×24=12(cm).
在Rt△COE中,设CO为r,则OE=r﹣8,
根据勾股定理得:122+(r﹣8)2=r2
解得r=13.
∴S⊙O =π×132=169π(cm2).

练习册系列答案
相关题目