题目内容
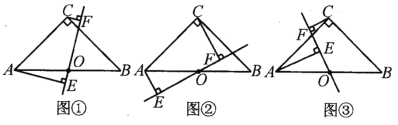
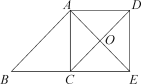
【题目】已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
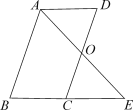
(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形 ACED是正方形.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,首先证明四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,∴OC=OD,
在△AOD和△EOC中,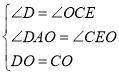 ,∴△AOD≌△EOC(AAS);
,∴△AOD≌△EOC(AAS);
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.
∵△AOD≌△EOC,∴OA=OE.
又∵OC=OD,∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.∴□ACED是菱形.
∵AB=AE,AB=CD,∴AE=CD.
∴菱形ACED是正方形.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目