题目内容
【题目】如图所示，抛物线y＝ax2+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b2﹣4ac＝0 ②a+b+c＞0 ③2a﹣b＝0④c﹣a＝3，其中正确的有_____．（填序号）
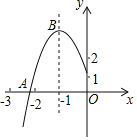
【答案】③④
【解析】
①根据图象与x轴的交点个数即可判断；
②根据x=3与x=1关于x=1对称，即可判断；
③根据顶点坐标即可判断；
④根据顶点坐标即可判断；．
解：∵图象和x轴有两个交点，
∴b2﹣4ac＞0，故①错误；
由于对称轴为x=1，
∴x=3与x=1关于x=1对称，
∵x=3时，y<0，
∴x=1时，y=a+b+c<0，故②错误；
∵﹣
＝﹣1，
∴2a﹣b＝0，故③正确；
∵顶点为B(1,3)，
∴y=ab+c=3，
∴y=a2a+c=3，
即ca=3，故④正确；
故答案为③④．
练习册系列答案
相关题目
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.
（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？
（2）如果先进行精加工，然后进行粗加工.
①试求出销售利润
元与精加工的蔬菜吨数
之间的函数关系式；
②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？
