题目内容
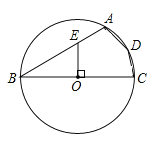
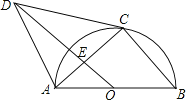
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠B=∠DCA,AD∥BC,连结OD,AC,且OD与AC相交于点E.
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为4,且![]() =
=![]() ,求tan∠DCA的值.
,求tan∠DCA的值.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接OC,易证∠DCA=∠OCB,由于∠ACO+∠OCB=90°,所以∠ACO+∠DCA=90°,即∠DCO=90°,从而可证CD与⊙O相切;
(2) 过点O作OF∥BC,交CD于点F,交AC于点G,由于△AED∽△GEO,再利用对应边成比例,设AD=5x,OG=2x,进一步证明△ADC∽△CAB,所以AC2=ADBC,所以AC=![]() ,最后根据锐角三角函数即可求出tan∠B的值.
,最后根据锐角三角函数即可求出tan∠B的值.
解:(1)连接OC,如下图所示:
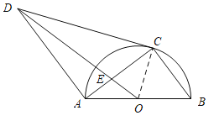
∵OC=OB,
∴∠OCB=∠B,
∵∠B=∠DCA,
∴∠DCA=∠OCB,
∵∠ACO+∠OCB=90°,
∴∠ACO+∠DCA=90°,
即∠DCO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
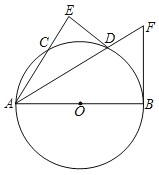
(2)过点O作OF∥BC,交CD于点F,交AC于点G,
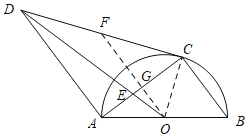
∵AD∥BC,
∴AD∥OG,
∴△AED∽△GEO,
![]() ,
,
设AD=5x,OG=2x,
∵∠ACB=90°,
∴由垂径定理可知:点G为AC的中点,
∴OG是△ACB的中位线,
∴BC=2OG=4x,
∵∠B=∠DCA,∠DAC=∠ACB=90°,
∴△ADC∽△CAB
∴![]() ,
,
∴AC2=AD×BC,
∴AC=![]() ,
,
∴tan∠B=![]() .
.
故答案为:tan∠B=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目