题目内容
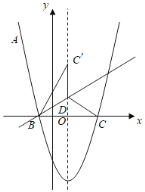
【题目】如图,抛物线y=![]() ﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
(1)求a的值及B、C两点坐标;
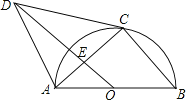
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△B![]() D,若点
D,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点D的坐标;
和点D的坐标;
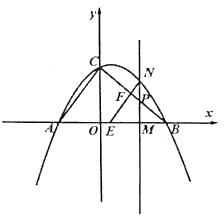
(3)设P(m,-3)是该抛物线上一点,点Q为抛物线的顶点,在x轴、y轴分别找点M、N,使四边形MNQP的周长最小,请求出点M、N的坐标.
【答案】(1)5;(-1,0),(3,0) (2)(1,![]() );(1,
);(1,![]() ) (3)(
) (3)(![]() ,0);(0,
,0);(0,![]() )
)
【解析】
(1)把A(-2,a)代入y=x2﹣2x﹣3可得a的值,分别 令y=0求出抛物线与x轴的交点坐标,从而可得B、C点坐标;
(2)设对称轴于BC的交点为E,先求出点C,点E坐标,可求BC=4,BH=CH=2,由折叠的性质可得BC'的长,由勾股定理可求C'H,DH的长,即可求解;
(4)作Q点关于y轴的对称点Q′(-1,-4),作点P(2,-3)关于x轴的对称点P′(2,3),连接Q′P′分别交x、y轴于点M、N,此时,四边形QPMN的周长最小,即可求解.
解:(1)把A(-2,a)代入y=x2﹣2x﹣3,得a=5;
当y=0时,x2﹣2x﹣3=0 解得x1=3, x2=-1
∵B点在C点左侧
∴B(-1,0),C(3,0)
(2)如图,设抛物线的对称轴与x轴交于点H,则H点的坐标为(1,0),BH=2,
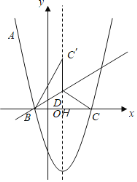
由翻折得C′B=CB=4,
在Rt△BHC′中,由勾股定理,得![]() ,
,
∴点C′的坐标为(1,2![]() ),tan
),tan![]() ,
,
∴∠C′BH=60°,
由翻折得∠DBH=![]() ∠C′BH=30°,
∠C′BH=30°,
在Rt△BHD中,DH=BHtan∠DBH=2tan30°=![]() ,
,
∴点D的坐标为(1,![]() ).
).
(3)如图2,
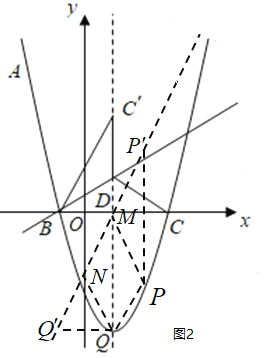
∵Q为抛物线的顶点,
∴Q(1,﹣4),
∴Q关于y轴的对称点Q'(﹣1,﹣4),
∵P(m,-3)在抛物线上,
∴P(2,﹣3),
∴点P关于x轴的对称点P'(2,3),
连接Q′、P′分别交x、y轴于点M、N,此时,四边形OPMN的周长最小,,
设直线Q′P′的解析式为y=kx+b,则有
![]() ,解得
,解得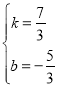 ,
,
∴直线P'Q'的解析式为y=![]() x﹣
x﹣![]() ,
,
当x=0时,y=﹣![]() ;当y=0时,x=
;当y=0时,x=![]() ;
;
∴M(![]() ,0),N(0,﹣
,0),N(0,﹣![]() ).
).