Question

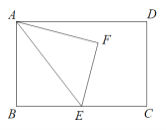
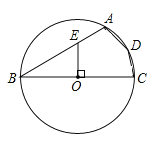
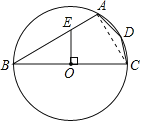
【题目】如图，四边形ABCD是⊙O的内接四边形，BC是⊙O的直径，OE⊥BC交AB于点E，若BE=2AE，则∠ADC =_________°．

Answer 1

【答案】150

【解析】

连接AC，证明△BOE∽△BAC，根据相似三角形的性质得到x、r的关系，根据余弦的定义求出∠B，根据圆内接四边形的性质计算，得到答案．

解：连接AC，

设⊙O的半径为r，AE=a，则BE=2a，

∵BC是⊙O的直径，

∴∠BAC=90°，

∵OE⊥BC，

∴∠BOE=90°，

∴∠BOE=∠BAC，又∠B=∠B，

∴△BOE∽△BAC，

∴，即，

整理得，r=x，

∴cosB=，

∴∠B=30°，

∵四边形ABCD是⊙O的内接四边形，

∴∠ADC=180°-∠B=150°，

故答案为：150．