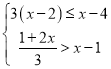题目内容
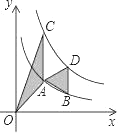
【题目】如图,点A,B在反比例函数![]() (x>0)的图象上,点C,D在反比例函数
(x>0)的图象上,点C,D在反比例函数![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )
A. 3 B. 4 C. 2 D. ![]()
【答案】A
【解析】
先求出点A,B的坐标,再根据AC∥BD∥y轴,确定点C,点D的坐标,求出AC,BD,最后根据,△OAC与△ABD的面积之和为![]() ,即可解答.
,即可解答.
解:∵点A,B在反比例函数y=![]() (x>0)的图象上,点A,B的横坐标分别为1,2,
(x>0)的图象上,点A,B的横坐标分别为1,2,
∴点A的坐标为(1,1),点B的坐标为(2,![]() ),
),
∵AC∥BD∥y轴,
∴点C,D的横坐标分别为1,2,
∵点C,D在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴点C的坐标为(1,k),点D的坐标为(2,![]() ),
),
∴AC=k-1,BD=![]()
![]() =
=![]() ,
,
∴S△OAC=![]() (k-1)×1=
(k-1)×1=![]() ,S△ABD=
,S△ABD=![]()
![]() ×(2-1)=
×(2-1)=![]() ,
,
∵△OAC与△ABD的面积之和为![]() ,
,
∴![]() +
+![]() =
=![]() ,
,
解得:k=3.
故选:A.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目