题目内容
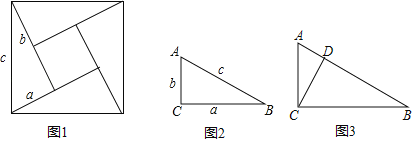
【题目】如图1所示,有四个同样大小的直角三角形,两条直角边分别为a、b,斜边为c,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于a、b、c的等式;
(2)利用(1)中发现的直角三角形中两直角边a,b和斜边c之间的关系,完成问题:如图2,在直角△ABC中,∠C=90°,且c=6,a+b=8,则△ABC的面积为 ;
(3)如图3所示,CD是直角△ABC中斜边上的高,试证明CD2=ADBD.
【答案】(1)c2=a2+b2;(2)7;(3)详见解析.
【解析】
(1)根据大正方形的面积的不同表示方法,即可得到于a,b,c的等式;
(2)根据(a+b)2=64,a2+b2=c2=36,即可得到ab=14,进而得出△ABC的面积;
(3)证明△ACD∽△CBD 即可得到结论.
(1)由题意得,c2=4×![]() ×ab+(b﹣a)2 即c2=a2+b2
×ab+(b﹣a)2 即c2=a2+b2
(2)由(1)得,c2=a2+b2=(a+b)2﹣2ab=64﹣2ab=36,
∴ab=14
∴S=![]() =7
=7
故答案为:7.
(3)由题可知,∠ACD=∠CBD
∠ADC=∠CDB
∠CAD=∠BCD
∴△ACD∽△CBD
∴![]() ,即CD2=ADBD.
,即CD2=ADBD.

练习册系列答案
相关题目