题目内容
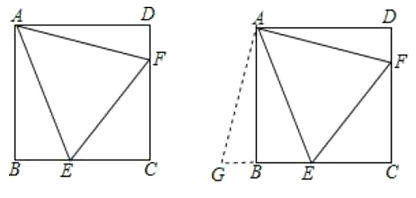
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上两点,
上两点,![]() ,过点
,过点![]() 作
作![]() ,且点
,且点![]() 为边
为边![]() 延长线上一点.
延长线上一点.
(1)![]() 吗?说明理由.
吗?说明理由.
(2)若线段![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
【答案】(1)见解析;(2)12;(3)EF=10
【解析】
(1)通过正方形的性质可得AB=AD、∠ABG =∠D,即可证明△GAB≌△FAD.
(2)通过证明△GAE≌△FAE(SAS)和△GAB≌△FAD,可得EF=GE和GB=DF,从而可得EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4,根据EC=BCBE可得EC=12(x4)=16x,根据勾股定理列方程求解即可.
(1)全等.
证明:∵四边形ABCD为正方形
∴AB=AD,∠ABE=∠D=90![]() ,
,
∴∠ABG =90![]() =∠D
=∠D
在△ABG和△ADF中,
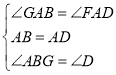
∴△GAB≌△FAD.
(2)∵∠BAD=90![]() ,∠EAF=45
,∠EAF=45![]()
∴∠DAF+∠BAE=45![]()
∵△GAB≌△FAD
∴∠GAB=∠FAD,AG=AF
∴∠GAB+∠BAE=45![]()
∴∠GAE=45
∴∠GAE=∠EAF
在△GAE和△FAE中
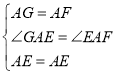
∴△GAE≌△FAE(SAS)
∴EF=GE.
∵△GAB≌△FAD
∴GB=DF
∴EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4.
∵EC=BCBE,
∴EC=12(x4)=16x.
在Rt△EFC中,依据勾股定理可知:
EF2=FC2+EC2,
即(16x) 2+82=x2,
解得:x=10.
∴EF=10.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目