题目内容
【题目】如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
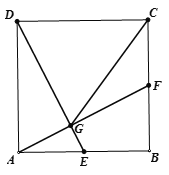
(1)求证:AF⊥DE;
(2)求证:CG=CD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题(1)正方形ABCD中,AB=BC,BF=AE,且∠ABF=∠DAE=90°,即可证明△ABF≌△DAE,即可得∠DGA=90°,结论成立.
(2)延长AF交DC延长线于M,证明△ABF≌△MCF,说明△DGM是直角三角形,命题得证.
试题解析:(1)∵四边形ABCD为正方形
∴AB=BC=CD=AD,∠ABF=∠DAE=90°,
又∵E,F分别是边AB.BC的中点
∴AE=![]() AB.BF=
AB.BF=![]() BC
BC
∴AE=BF.
在△ABF与△DAE中,
 ,
,
∴△DAE≌△ABF(SAS).
∴∠ADE=∠BAF,
∵∠BAF+∠DAG=90°,
∴∠ADG+∠DAG=90°,
∴∠DGA=90°,即AF⊥DE.
(2)证明:延长AF交DC延长线于M,

∵F为BC中点,
∴CF=FB
又∵DM∥AB,
∴∠M=∠FAB.
在△ABF与△MCF中,

∴△ABF≌△MCF(AAS),
∴AB=CM.
∴AB=CD=CM,
∵△DGM是直角三角形,
∴GC=![]() DM=DC.
DM=DC.

【题目】校团委决定对甲、乙、丙三位候选人进行民主投票、笔试、面试考核,从中推选一名担任学生会主席.已知参加民主投票的学生为200名,每人当且仅当推荐一名候选人,民主投票结果如下扇形统计图所示,笔试和面试的成绩如下统计表所示.
甲 | 乙 | 丙 | |
笔试 | 78 | 80 | 85 |
面试 | 92 | 75 | 70 |
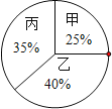
(1)甲、乙、丙的得票数依次是______、______、______;
(2)若民主投票得一票记1分,学校将民主投票、笔试、面试三项得分按3:4:3的比例确定三名候选人的考核成绩,成绩最高当选,请通过计算确定谁当选.