题目内容
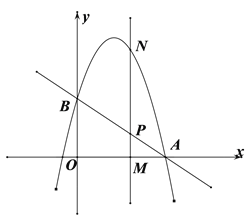
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
【答案】⑴![]() ,
, ![]() ⑵
⑵![]() ⑶有两解,N点在AB的上方或下方, m=
⑶有两解,N点在AB的上方或下方, m=![]() 与m=
与m=![]()
【解析】整体分析:
(1)把A(3,0)代入y=kx+2中求k值,把x=0代入y=kx+2,求出B点的坐标,由A,B的坐标求二次函数的解析式;(2)①用含m的式子表示出NP的长,由平行四边形的性质得OB=PN列方程求解;②连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H, 设GH=BH=t,由![]() ,用t表示AH,AG,由AB=
,用t表示AH,AG,由AB=![]() ,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
解:⑴![]() ,
,
二次函数的表达式为![]()
⑵如图,设M(m,0),
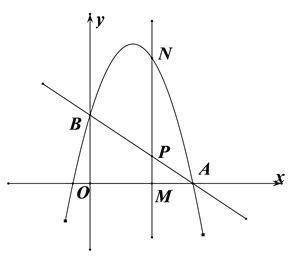
则p(m, ![]() ),N(m,
),N(m, ![]()
![]() =
=![]()
=![]()
由于四边形OBNP为平行四边形得PN=OB=2,
解方程![]() .
.
即![]()
⑶有两解,N点在AB的上方或下方,m=![]() 与m=
与m=![]() .
.
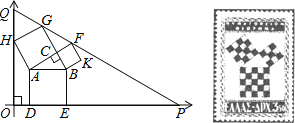
如图连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
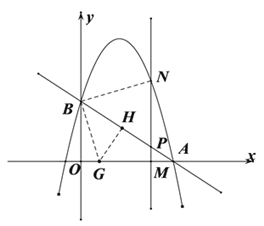
由![]() 得
得![]() ,
,
从而设GH=BH=t,则由![]() ,得AH=
,得AH= ![]() ,
,
由AB=t+ ![]() =
=![]() ,解得t=
,解得t=![]() ,
,
从而OG=OA-AG=3-![]() =
=![]() .即G(
.即G(![]() )
)
由B(0,2),G(![]() )得
)得![]() .
.
将![]() 分别与
分别与![]() 联立,
联立,
解方程组得m=![]() ,m=
,m=![]() .
.
故m=![]() 与m=
与m=![]() .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.