题目内容
【题目】已知:如图所示,在平面直角坐标系xOy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动,设点P、点Q的运动时间为t(s).
(1)当t=1 s时,求经过点O,P,A三点的抛物线的解析式;
(2)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(3)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.

【答案】(1)![]() ;(2)t=3;(3)
;(2)t=3;(3)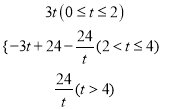 .
.
【解析】试题分析:(1)可求得P点坐标,由O、P、A的坐标,利用待定系数法可求得抛物线解析式;
(2)用t可表示出BP和AQ的长,由![]() 可得到关于t的方程,可求得t的值;
可得到关于t的方程,可求得t的值;
(3)当点Q在线段OA上时, ![]() ;当点Q在线段OA上,且点P在线段CB的延长线上时,由相似三角形的性质可用t表示出AM的长,由S=S四边形BCQM=S矩形OABC-S△COQ-S△AMQ,可求得S与t的关系式;当点Q在OA的延长线上时,设CQ交AB于点M,利用
;当点Q在线段OA上,且点P在线段CB的延长线上时,由相似三角形的性质可用t表示出AM的长,由S=S四边形BCQM=S矩形OABC-S△COQ-S△AMQ,可求得S与t的关系式;当点Q在OA的延长线上时,设CQ交AB于点M,利用![]() 可用t表示出AM,从而可表示出BM,
可用t表示出AM,从而可表示出BM, ![]() ,可求得答案.
,可求得答案.
试题解析:(1)依题意得,A(4 ,0),B(4,3).
当t=1 s时,CP=2,
![]()
设经过O、P、A三点抛物线的解析式为y=ax(x-4),将P(2,3)代入解析式中,则有
2×(2-4)a=3,
![]()
![]()
【一题多解】依题意得,A(4,0),B(4,3).
当t=1 s时,CP=2,∴P(2,3).
设经过O、P、A三点抛物线的解析式为y=ax2+bx+c,将O,P,A三点代入得
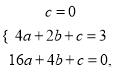
解得: 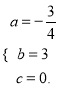
∴抛物线的解析式为![]()
(2)如解图①,设线段PQ与线段BA相交于点M,依题意有:CP=2t,OQ=t,
∴BP=2t-4,AQ=4-t.
∵CB∥OA,
∴△BMP∽△AMQ,
![]()
∴BP=2AQ,即2t-4=2(4-t),∴t=3;
(3) 当0≤t≤2时,如解图②,![]()
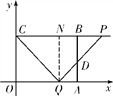
当2<t≤4,如解图③,设线段AB与线段PQ相交于点D,过点Q作QN⊥CP于点N,则△BDP∽△NQP,
![]()
又∵NQ=CO=3,BP=CP-CB=2t-4,且NP=CP-CN=CP-OQ=2t-t=t,
![]()
![]()
∴S=S四边形CQDB=S△CQP-S△BDP,
![]()
 ③
③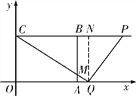 图④
图④
当t>4时,如解图④,设线段AB与线段CQ相交于点M,过点Q作QN⊥CP于点N,则△CBM∽△CNQ,
![]()
又∵CB=OA=4,CN=OQ=t,NQ=3,
![]()
![]()
![]()
∴S=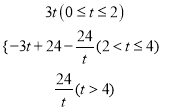 .
.

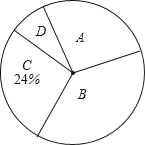
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?